You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Poroacoustics node introduces several fluid models for modeling the propagation of acoustic waves in porous materials. After some general remarks about fluid models and the rigid and limp regime approximations, these models are discussed in this section:
The poroacoustics fluid models are equivalent fluid models that mimic the behaviors of a full Poroelastic Material model, which is defined by Biot’s theory. A poroacoustics fluid model is based on describing the frequency-dependent effective fluid density
ρ(
ω) and the effective fluid bulk modulus
K(
ω) of the combined equivalent fluid-solid system (saturating fluid and porous matrix). The description of these models includes the losses associated with the propagation of acoustic waves in porous materials. An
equivalent fluid model is computationally less demanding than the full poroelastic model. However, it is only physically correct for certain choices of material parameters. Most poroacoustic models are only valid in the rigid or limp porous matrix approximations.
In the rigid porous matrix limit, the matrix is assumed to be so stiff that it does not move (sometimes referred to as a
motionless skeleton model). In this case it is assumed that in Biot’s theory
u =
0, which yields a wave equation with complex density and bulk modulus. In a rigid porous material the Biot-Willis coefficient is equal to the porosity
αB =
εP. All the poroacoustic fluid models are based on defining the rigid effective density
ρrig (see
Ref. 9).
The limp porous matrix limit is the opposite of the rigid assumption. It is used to model materials where the stiffness of solid phases (the porous matrix) is so weak that it cannot support free, structure-borne wave propagation (neither longitudinal nor transverse). That is, the stiffness (in vacuo bulk stiffness) is very small compared to air such that the solid phase motion becomes acoustically significant. If it is light enough, the solid phase still moves because it is “dragged along” by the fluid motion; a limp porous material model is also an equivalent fluid model because it only features a single longitudinal wave type. Typically, the limp assumption can be applied to very light weight fibrous materials (less than 10 kg/m
3) if these are not stiffened by the injection of binder material. In the limp case, it is assumed that the stress tensor vanishes and that in Biot’s theory, the Biot-Willis coefficient is
αB = 1. The limp density is related to the rigid density by a mixture model (see
Ref. 10)

where ρf is the fluid density,
ρd is the drained porous matrix density,
ρav is the average effective density, and
ρlimp is the resulting effective limp density.
(2-39)
 ,
,where α0 is the isobaric thermal expansion coefficient,
T0 is the background quiescent temperature,
ρ0 is the background quiescent density,
Cp is the specific heat at constant pressure,
β0 is the isothermal compressibility (inverse isothermal bulk modulus
KT), and
c is the speed of sound. This result comes from thermodynamics.
(2-40)
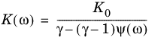
for any of these models, where the frequency response Ψ(
ω) is specific to each model. Consequently, the following derivation is sufficient to show the general result.
(2-41)
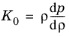 .
.A relationship between the pressure p and the density
ρ is needed to define the effective bulk modulus, and the equation of state provides such a relationship. Instead of relying on the ideal gas equation, we here use the following general equation of state
(2-42)
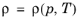
which merely stipulates that the density ρ is a function of both pressure
p and temperature
T. The temperature-dependence is nonnegligible since we are dealing with small pores, and acoustics in porous materials belong to thermoviscous acoustics (see
Thermoviscous Acoustics Interfaces). Assuming the acoustic fields are small harmonic perturbations (denoted by a subscript 1) about a quiescent reference state (denoted by subscript 0)
(2-43)
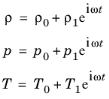
(2-44)
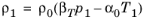
where βT is the isothermal compressibility.
(2-45)
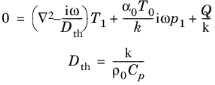
where Dth is the thermal diffusivity,
k is the thermal conductivity, and
Q is a volumetric heat source. To proceed with the solution of this equation, it is generally assumed that (
i) the pore can be modeled as a hollow cylinder, (
ii) the contributions from radial variations dominate over axial variations so it suffices to solve the radial problem while assuming no axial variations
Ref. 9, and (
iii) the pore radius is much smaller than the wavelength, whereby the pressure does not change noticeably across the radius. By these assumptions the pressure
p1 can be treated as a constant in
Equation 2-45 and the equation has only radial variations:
(2-46)
 .
. (2-47)
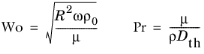
where Wo is the Womersley number (see the note below), and Pr is the Prandtl number, measuring the relative width of the viscous boundary layer thickness to the thermal boundary layer thickness.
With the solution from Equation 2-46, the pressure can now be expressed as a function of the density using the first-order equation of state
Equation 2-44:
(2-48)
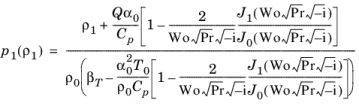
(2-49)

where the ratio of specific heats γ is defined in
Equation 2-39 for a general fluid and
K0 is the isentropic bulk modulus of the fluid. This formula
Equation 2-49 is mathematically equivalent to the normal Zwikker-Kosten formula for the equivalent bulk modulus (see
Ref. 15), but it has been
derived for a general fluid and not just an ideal gas.
(2-50)
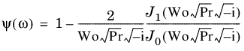
with the Womersley number Wo containing the frequency dependence.
|
|
The Womersley number Wo measures the influence of viscous effects relative to the oscillation frequency ω. For 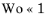 viscosity dominates and the velocity profile is the well-known Poiseuille parabola, while in the Helmholtz regime for 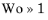 the velocity profile is plug-like with a very small boundary layer close to the walls.
|
where ρf is the fluid density,
f is the frequency, and
Rf is the flow resistivity. Several predefined sets of the coefficients
Ci exist. They are the classic Delany-Bazley model, the Miki model (see
Ref. 9, section 2.5 and ), the Qunli, several variants of the Mechel model for different configurations, the Komatsu model, and a so-called Modified Champoux and Allard model.
These are all empirical models based on fitting the two complex functions to measured data for the complex wave number
kc and complex specific acoustic impedance
Zc. All the models are applicable for materials with a porosity
εp close to 1. The applicability of the different model parameters is listed in
Table 2-10. See also
Ref. 23 for further details.
where Hr is the hydraulic radius of the pores (for straight cylindrical pores
Hr = a = radius) and Wo is the Womersley number (see
Equation 2-47 and the note below). Wo is related to the ratio between viscous penetration depth
δv and the hydraulic radius.
δv gives the scale of the viscous boundary layer thickness (see
Theory Background for the Thermoviscous Acoustics Branch for details). The bulk modulus is given by
where pA denotes the ambient pressure,
ρf the fluid density,
γ the ratio of specific heat,
Pr the Prandtl number, µ the dynamic viscosity,
Cp the heat capacity at constant pressure, and
k the coefficient of thermal conduction.
J0 and
J1 are Bessel functions of the first kind. The factor
γ pA is the isentropic bulk modulus (
K0 =
γ pA). The free parameters of the pores are the porosity
εP and the hydraulic radius
Hr.
The Attenborough model is also based on the cylindrical-like pore assumption. It is a so-called four parameter semi-empirical model. The model is an extension of the Zwikker-Kosten model and adds two more input parameters. It accounts for the tortuosity (high frequency limit) 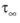
, which is related to the orientation of the pores relative to the propagation direction. The hydraulic diameter of the pores is replaced by an expression that includes the flow resistivity
Rf, and a fitting parameter
b, (this parameter is related to the anisotropy of the pores). See
Ref. 9 and
Ref. 16. The equivalent density and bulk modulus are defined as
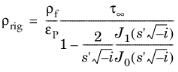
where pA denotes the ambient pressure,
ρf the fluid density,
γ the ratio of specific heat,
Pr the Prandtl number, µ the dynamic viscosity,
Cp the heat capacity at constant pressure, and
k the coefficient of thermal conduction.
J0 and
J1 are Bessel functions of the first kind. The variable
s'
(anisotropy factor) is derived from other material parameters and is related to the Womersley number (see
Equation 2-47):
Here, ω denotes the angular frequency. The four parameters needed (when the fluid is air at room temperature) are the porosity
εP, the tortuosity
τ∞, flow resistivity
Rf, and the fitting parameter
b (dimensionless, close to 1). The fitting parameter
b is tabulated for certain well-defined pore cross-sections in
Table 2-11.
with δv the viscous penetration depth. This length is related to the pores’ circular cross section radius
R (for a cylinder) and the thickness of the viscous boundary layer. The parameter
b = 1/
s, where
s is the viscous characteristic length parameter. See the following models:
Note that the tortuosity is related to the angle θ between the cylindrical pores and the direction of propagation of the wave, by
where τvor denotes the vorticity-mode relaxation time,
τent the entropy-mode relaxation time,
ρ∞ the infinity frequency limit for the density,
K∞ the infinity frequency limit for the bulk modulus, and
γ is the ratio of specific heats. These are the four free parameters. With appropriate choices for the relaxation parameters, the Wilson model can be fitted to mimic all the models described here. For example, setting
τvor =
2.54/
Rf and
τent =
3.75/
Rf, the equations mimic the Delany-Bazley model (see Cox and D’Antonio Sec. 5.4.4,
Ref. 18).
Here τ∞ denotes the (high frequency limit) tortuosity (it is called
q2 in the Wilson’s paper
Ref. 17),
εp the porosity,
ρf the fluid density,
l a characteristic pore dimension, and
Pr is the Prandtl number.
Here τ∞ is the tortuosity factor (high frequency limit),
ρf is the fluid density,
εp is the porosity,
Rf is the flow resistivity,
μ is the dynamic viscosity,
pA is the quiescent pressure,
γ is the ratio of specific heats,
Lv is the viscous characteristic length,
Lth is the thermal characteristic length, and
Pr is the Prandtl number. The viscous characteristic length is related to the viscous characteristic length parameter
s by
Here s is a pore geometry dependent factor between 0.3 and 3.0 (for example 1 for circular pores, 0.78 for slits)
|
|
The viscous Lv and thermal Lth characteristic lengths are also sometimes denoted by Λ and Λ’, respectively.
|
|
|
Porous Absorber: Application Library path Acoustics_Module/Building_and_Room_Acoustics/porous_absorber
|
with the introduction of the new parameter, k’0, which is the static thermal permeability (SI unit: m
2). For measurements and details of this parameter see
Ref. 11 and
Ref. 12 for examples.
where the new parameter is the static viscous tortuosity τ0 (dimensionless). The viscous permeability is defined as
k0 = μ/Rf (SI unit: m
2).
|
|
In Ref. 9 (equation 5.32), P is called b, k0 is called q0, and Pr is called B2.
|
|
|
In Ref. 9 (equation 5.35), 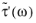 is called α '( ω), and P’ = 1.
|
where the subscript “gr” pertains to the grains and the subscript “f” to the saturating fluid. The porosity is denoted εp, the observed mixture density
ρmix, the tortuosity
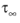
, the dynamic viscosity
μ, the angular frequency
ω, and the permeability of the sediments
κ. The function
F is a function of the Womersley number
Wo defined as
where Jn(
x) is the Bessel function of the first kind of order n and
Hr is the hydraulic radius. Based on these the effective complex speed of sound and density are given as
where θf,
Kf, and
ρf, are the fluid’s volume fraction, adiabatic bulk modulus, and density, respectively; and
θi,
Ki, and
ρi, are the inclusion’s volume fractions, adiabatic bulk moduli, and densities, respectively. And again the complex speed of sound and density are defined as

 ,
, .
.