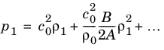The Nonlinear Westervelt Equation

To extend the validity of the small perturbation wave equation to finite amplitude waves, nonlinear effects need to be taken into account. The first idea is to expand the density pressure relation to second order to include the effect of finite amplitude waves. This gives

where we have kept the subscript “1” to highlight the acoustic perturbation quantities and a subscript “0” for the quiescent quantities. See Ref. 6 and 42 for details. The quantity B/A is the parameter of nonlinearity (see Ref. 51). This expression basically means that the different parts of the acoustic pressure wave travel at different speeds.

Inserting the above into the governing Equation 2-7 (retaining the dissipative terms) will lead to the full nonlinear second-order wave equation. This is the nonlinear equivalent to Equation 2-8 (or actually the nonlinear equivalent to the full equations of thermoviscous acoustics). Next assume that boundary layer effects can be disregarded and cumulative nonlinear effects dominate local nonlinear effects, for example, when the propagation distance is greater than the wavelength. This leads to the well-known Westervelt equation (see Ref. 42)

Here we have eliminated the density fluctuations and then removed the subscripts. Hence, pt is the (total) acoustic pressure, ρ is the quiescent density, δ is the diffusivity of sound, and β is the coefficient of nonlinearity (related to the parameter of nonlinearity B/A).

The Westervelt equation supports the propagation of shocks. Shocks can be hard to capture numerically and require the addition of stabilization. This can, for example, be done by adding diffusivity near the shock location. One method (used in COMSOL) is to add an effective diffusivity term that reads

The highest artificial damping is achieved where the acoustic pressure increases or decreases the most rapidly. It reaches its maximal values where the pressure endures discontinuities, that is, where shocks arise. Thus this technique provides a shock-capturing stabilization. See Ref. 52 for more details. Specify the so-called q-Laplacian exponent q and the so-called q-Laplacian factor κ to get the desirable amount of artificial damping. Note that the damping must not be too high nor too low. The particular values of q and κ depend on the material and the input signal frequency. The two parameters that control the stabilization require manual tuning. A suggested approach is to use a simple 1D model to tune the parameters based on fluid material properties and frequency content.