Initial Conditions: Direction
There are several options available for specifying the initial direction of rays. These options work by assigning values to the degrees of freedom corresponding to the wave vector k (SI unit: rad/m) of each ray.
Expression
The default is to enter an expression for the Ray direction vector L0 (dimensionless). This vector need not have a magnitude of unity because it is always normalized automatically. The initial wave vector is
where ω (SI unit: rad/s) is the angular frequency and c (SI unit: m/s) is the speed of sound in the medium.
Spherical
When Spherical is selected the initial wave vectors are sampled from a distribution in wave vector space at each release point. The number of rays released from each point is usually equal to the specified value Nw (dimensionless), although it may be larger if the initial values of any auxiliary dependent variables are also sampled from a distribution.
In 2D the initial wave vector components are
where θ goes from 0 to 2π in Nw steps. In 3D the initial wave vector components are sampled according to the expressions
The azimuthal angle 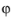is uniformly distributed from 0 to 2π. The polar angle θ is sampled from the interval [0, π] with probability density proportional to sin θ. The polar angle is arbitrarily chosen as the angle that the initial wave vector makes with the positive z-axis, but any direction could be chosen because the sphere is isotropic. Therefore each ray subtends approximately the same solid angle in wave vector space.
Hemispherical
The Hemispherical option is the same as the Spherical option, except that in 2D θ goes from 0 to π and in 3D θ goes from 0 to π/2. The angle is measured from the direction given by the Hemisphere axis setting.
Conical
The Conical option is the same as the Spherical option, except that θ goes from 0 to α. The angle is measured from the direction given by the Cone axis setting.
Lambertian
The Lambertian option releases rays within a hemisphere in 3D, but the probability distribution function is different from that of the Hemispherical option. Recall that for an isotropic hemispherical distribution the polar angle θ has a probability density proportional to sin θ; for the Lambertian distribution the probability density is instead proportional to sin θ cos θ. Because of this extra cosine term, distributions following this probability density are said to follow Lambert’s cosine law.