The Porous, Free boundary condition is the default for the porous matrix. It means that the displacement of the porous matrix in
Equation 3-11 is unconstrained, so it can move freely without experiencing any loads.
The sound soft boundary condition for acoustics creates a boundary condition for
Equation 3-12 where the acoustic pressure vanishes, so it sets
pf = 0.
For a given fluid pressure p0 on the boundary, set the pressure in
Equation 3-12 to
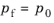
. Since the fluid pressure is set to
p0, the normal stress on the porous matrix in
Equation 3-11 reduces to
For a rigid porous matrix αB = εp, the load is equivalent to
For a prescribed displacement u0 at the boundary, set the displacement of the porous matrix in
Equation 3-11 as
u = u0 and assume a sound-hard (impervious) boundary for the fluid pressure in
Equation 3-12:
For a prescribed velocity v0 at the boundary, set the displacement of the porous matrix in
Equation 3-11 as
For a prescribed acceleration a0 at the boundary, set the displacement of the porous matrix in
Equation 3-11 as
The normal displacement of the porous matrix in Equation 3-11 is constrained, but the porous matrix is free to move in the tangential direction
For a prescribed load FA at the boundary, suppose that one side of the septum is fixed to the porous matrix and the other side bears the load.
A septum is a very limp and thin impervious layer with surface density ρsep. Since the septum can be seen as a boundary mass density, this boundary condition is achieved by setting an effective load
FS = FA + ρsepω2u on the porous matrix, so the normal stress in
Equation 3-11 reduces to