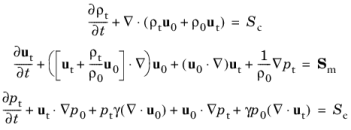Linearized Euler Model

Use the to set up the governing equations, define the background mean flow, the ideal gas fluid properties, and select gradient term suppression stabilization (advanced physics option), if needed. The governing equations solved are (in the time domain):

where ρt, ut, and pt are the acoustic perturbations to the density, velocity, and pressure, respectively. The subscript “t” refers to the fact that the acoustic variables are the total fields, that is, the sum of possible Background Acoustic Fields and the scattered fields.

In the frequency domain, the time derivatives of the dependent variables is replaced by multiplication with iω. The variables with a zero subscript are the background mean flow values, γ is the ratio of specific heats. The right-hand-side source terms Sc, Sm, and Se are zero per default. They can be defined in the Domain Sources node. Details about the physics solved and references are found in the Theory Background for the Aeroacoustics Branch section.

In order to model the influence of the background mean flow on the propagation of the acoustic waves in the fluid, the background mean flow temperature T0, absolute pressure p0, and velocity field u0 need to be defined.

Select (the default), , or a variable defined by a flow simulation performed using the CFD Module. By default they are set to the quiescent background conditions of air. All the background flow parameters can also be constants or analytical expressions functions of space.

	When modeling aeroacoustics it is important how the Mapping Between Fluid Flow and Acoustics Mesh is done from a numerical perspective.

	Details about the Model Input and the Default Model Inputs are found in the Global and Local Definitions chapter of the COMSOL Multiphysics Reference Manual.

Enter values for the T0 (SI unit: K), p0 (SI unit: Pa), and u0 (SI unit: m/s). The defaults are 293.15 K, 1 atm, and 0 m/s, respectively.

Note that the also needs to be defined or entered in the section below.

Select an option for the ρ0 (SI unit: kg/m3) — (the default), , (default value 1.2 kg/m3), or it can be picked up from a flow interface, for example, from a High Mach Number Flow model as . As the flow is assumed to be an ideal gas, the background density ρ0 is readily defined as

where Rs is the specific gas constant.

Define the remaining fluid properties necessary. Select the : (the default) or . The defaults take values or for enter another value or expression:

•

Mn (SI unit: g/mol). The default is 28.97 g/mol), which calculates Rs = R/Mn, where R is the gas constant.

Select an option from the γ list: (the default) or . The defaults take values or for enter another value or expression:

•

Cp (SI unit: J/(kg⋅K)). The default is 1005.4 J/(kg·K)), which calculates γ = Cp /(Cp − Rs).

When the linearized Euler (LE) equations are solved in the time domain (or in the frequency domain with an iterative solver), linear physical instability waves can develop, the so-called Kelvin-Helmholtz instabilities. They are instabilities that grow exponentially because no losses exist in the LE equations (no viscous dissipation and no heat conduction). They are also naturally limited by nonlinearities in the full Navier-Stokes flow equations. The terms responsible for the instabilities are typically the reactive terms in the governing equations. It has been shown that in some problems the growth of these instabilities can be limited, while the acoustic solution is retained, by canceling terms involving gradients of the mean flow quantities. This is known as gradient terms suppression (GTS) stabilization.

More details are available in Ref. 9, Ref. 10, Ref. 11, and in the Theory Background for the Aeroacoustics Branch section.

All the aeroacoustic specific terms can be disabled. They are grouped into Reactive terms and Convective terms. Select the following check boxes to activate the applicable gradient term suppression (GTS):