This example describes the pressure-wave propagation in a muffler for an internal combustion engine. The approach used here is generally applicable to analyzing the damping of propagating pressure waves as well as determining the transmission properties of a given system. The model uses the port boundary conditions to model the inlet and outlet of the muffler. The model shows how to analyze both inductive and resistive damping in pressure acoustics. The main output is the transmission loss for the frequency range 50 Hz–1500 Hz. It is represented both as a continuous curve and given in 1/3 octave bands.

where ρ is the density, c is the speed of sound, and ω gives the angular frequency. The subscript c refers to that these can be complex valued.

In the absorbing glass wool, modeled as a Poroacoustics domain, the damping enters the equation as a complex speed of sound, cc = ω/kc, and a complex density, ρc = kc Zc/ω, where kc is the complex wave number and Zc equals the complex impedance. This is a so-called equivalent fluid model for the porous domain where the losses are modeled in a homogenized way.

For a highly porous material with a rigid skeleton, the classical empirical Delany and Bazley model estimates these parameters as functions of frequency and flow resistivity. Using the original coefficients of Delany and Bazley (Ref. 1), the expressions are

where Rf  is the flow resistivity, and where ka = ω/ca and Za = ρa  ca are the free-space wave number and impedance of air, respectively. This model is the default selected for the Delany-Bazley-Miki model in the Poroacoustics domain feature. You can find flow resistivities in tables, see for example Ref. 3 or by measuring it. For glass-wool-like materials, Bies and Hansen (Ref. 2) give an empirical correlation

where ρap is the material’s apparent density and dav is the mean fiber diameter. This model uses a lightweight glass wool with ρap = 12 kg/m3 and dav = 10 μm.

The pressure distribution in the absorptive muffler without the lining material is shown in Figure 9 for the frequency f = 1500 Hz. From the figure, it is seen that at this frequency not only longitudinal standing waves exist but also transverse modes are present.

An important parameter for a muffler is the transmission loss or attenuation. It is defined as the ratio between the incoming and outgoing acoustic energy. The attenuation or transmission loss L (in dB) of the acoustic energy is defined by

Here Pin and Pout denote the incoming power at the inlet and the outgoing power at the outlet, respectively. These values are readily defined by the port boundary conditions as acpr.port1.P_in and acpr.port2.P_out and can be directly used in postprocessing.

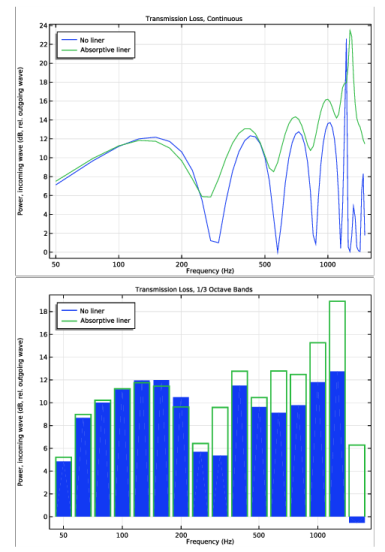
Figure 10 (top and bottom) shows the result of a parametric frequency study. The two graphs represent the case of an empty muffler without any absorbing lining material (blue lines) and the case with a layer of glass wool lining on the chamber’s walls (green lines). The first four dips are due to longitudinal resonances. In the muffler with absorbing lining, the dips are still present, but the general trend is that the higher the frequency, the better the damping. In the top figure, the transmission loss is depicted as a continuous curve (pure tone sweep) while it is depicted in 1/3 octave bands in the bottom figure. Both graphs are created using the Octave Band Plot of the Acoustics Module.

The graph for the undamped muffler shows that damping works rather well for most low frequencies. At frequencies higher than approximately 1250 Hz, the plot’s behavior is more complicated and there is generally less damping. This is because the tube supports not only longitudinal resonances but also cross-sectional propagating modes, for such frequencies. Not very far above this frequency a whole range of modes that are combinations of this propagating mode and the longitudinal modes participate, making the damping properties increasingly unpredictable. For an analysis of these modes, see the related model Eigenmodes in a Muffler. The glass-wool lining improves attenuation at the resonance frequencies as well as at higher frequencies.

The flow of energy in the muffler without the liner is shown in Figure 11 at 1500 Hz. The plot represents the intensity field depicted as streamlines. The intensity field is per definition the time average of the energy flux (instantaneous intensity) and thus represents the average energy flow in the system: here from the inlet to the outlet. Change between solutions and frequencies to study and visualize the sound-absorbing properties of the muffler.