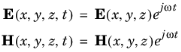Using the relation εr =
n2, where
n is the refractive index, the equation can alternatively be written
where c0 is the speed of light in vacuum.
When the equation is written using the refractive index, the assumption is that μr =
1 and
σ = 0 and only the constitutive relations for linear materials are available. When solving for the scattered field the same equations are used but
E = Esc + Ei and
Esc is the dependent variable.
For The Electromagnetic Waves, Beam Envelopes Interface the electric field is written as a product of an envelope function
E1 and a rapidly varying phase factor with a prescribed wave vector
k1,
When inserting this expression into Equation 3-1, the following wave equation for the electric field envelope
E1 is obtained
It is assumed that the envelope function E1 has a much slower spatial variation than the exponential phase factor. Thus, the mesh can be much coarser when solving
Equation 3-2 than when solving
Equation 3-1. Thereby it is possible do simulation on domains that are much larger than the wavelength. Notice, however, that the assumption of a slowly varying envelope function is never implemented in
Equation 3-2. Thus, the solution of
Equation 3-2 is as exact as the solution of
Equation 3-1.
The spatial parameter, α = δz + jβ = −λ, can have a real part and an imaginary part. The propagation constant is equal to the imaginary part, and the real part,
δz, represents the damping along the propagation direction. When solving for all three electric field components the allowed anisotropy of the optionally complex relative permittivity and relative permeability is limited to:
where z is the unit vector in the out-of-plane
z-direction.
where ϕ is the unit vector in the out-of-plane
ϕ-direction.
The TM waves polarization has only one magnetic field component in the z direction, and the electric field lies in the modeling plane. Thus the time-harmonic fields can be obtained by solving for the in-plane electric field components only. The equation is formally the same as in 3D, the only difference being that the out-of-plane electric field component is zero everywhere and that out-of-plane spatial derivatives are evaluated for the prescribed out-of-plane wave vector dependence of the electric field.
As the field propagates in the modeling xy-plane a TE wave has only one nonzero electric field component, namely in the
z direction. The magnetic field lies in the modeling plane. Thus the time-harmonic fields can be simplified to a scalar equation for
Ez,
To be able to write the fields in this form, it is also required that εr,
σ, and
μr are nondiagonal only in the
xy-plane.
μr denotes a 2-by-2 tensor, and
εrzz and
σzz are the relative permittivity and conductivity in the
z direction.
A TM wave has a magnetic field with only a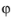 
component and thus an electric field with components in the rz-plane only. The equation is formally the same as in 3D, the only difference being that the
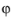
component is zero everywhere and that spatial derivatives with respect to
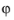
are evaluated for the prescribed azimuthal mode number dependence of the electric field.
where ε' is the real part of
εr, and all losses (dielectric and conduction losses) are given by
ε''. The dielectric loss model can also single out the losses from finite conductivity (so that
ε'' only represents dielectric losses) resulting in:
For the physics interfaces in the Wave Optics Module, the refractive index is the default electric displacement field model . In materials where
μr is 1, the relation between the complex refractive index
The parameter κ represents a damping of the electromagnetic wave. When specifying the refractive index, conductivity is not allowed as an input.
,
direction, and the magnetic field lies in the modeling plane. Given these constraints, the 3D equation can be simplified to a scalar equation for 
. To write the fields in this form, it is also required that εr and μr are nondiagonal only in the rz-plane. μr denotes a 2-by-2 tensor, and 
and 
are the relative permittivity and conductivity in the 
direction.
.
.
.
,
,
are evaluated for the prescribed azimuthal mode number dependence of the electric field.