You are viewing the documentation for an older COMSOL version. The latest version is
available here.
For a linear elastic material, Hooke’s law relates the undamaged stress tensor
σun to the elastic strain tensor:
(3-60)

here, 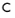 is the fourth order elasticity tensor
is the fourth order elasticity tensor, “:” stands for the double-dot tensor product (or double contraction). The elastic strain
εel is the difference between the total strain
ε and all inelastic strains
εinel. There may also be an extra stress contribution
σex, with contributions from initial, external or viscoelastic stresses.
For the scalar damage models, the damaged stress tensor
σd is computed from the undamaged stress as
(3-61)
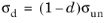
(3-62)
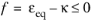
here, εeq is the equivalent strain, a scalar measure of the elastic strain; and
κ is a state variable. The evolution of the state variable
κ follows the Kuhn-Tucker loading/unloading conditions
In this formulation, κ is the maximum value of
εeq in the load history. The damage variable
d is then computed as a function of the state variable
κ and other parameters.
Different damage models use different definitions for the equivalent strain εeq. The
Rankine damage model defines the equivalent strain from the largest undamaged principal stress
σp1 as
(3-63)
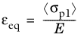
here, the symbol “<>” are the Macaulay brackets, and E is Young’s modulus. The Macaulay brackets are used since in this formulation only tensile (positive) stresses cause damage.
The Smooth Rankine damage model defines the equivalent strain from the three undamaged principal stresses
(3-64)
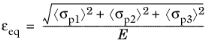
The Euclidean Norm of the elastic strain tensor can also be used as a measure for the equivalent strain
(3-65)
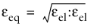
For Mazars damage for concrete, it is also possible to select from
Mazars or
Modified Mazars equivalent strain. For Mazars equivalent strain is defined as
(3-66)
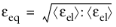
In the Modified Mazars equivalent strain (Ref. 2 and
Ref. 3), a correction factor
γ is added to improve the approximation of the failure surface of concrete in multiaxial compression.
(3-67)
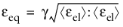
It is also possible to apply a User defined expression for defining the equivalent strain as a function of undamaged stress, stress components or strains.
(3-68)
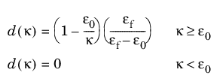 ,
,Here, ε0 denotes the onset of damage, computed from the tensile strength
σts and Young’s modulus
E, so that
ε0 = σts/E. The parameter
εf is derived from parameters such as the tensile strength, the characteristic element size
hcb and the fracture energy per unit area
Gf, or the fracture energy per unit volume
gf.
(3-69)

The Exponential strain softening law defines the damage evolution from
(3-70)
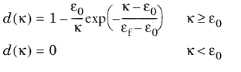
(3-71)
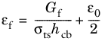
The Mazars damage for concrete utilizes two different damage evolution laws, one for tensile damage and another for compressive damage. These two damage functions are combined as
(3-72)
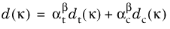
here, αt and
αc are weight functions depending on the current stress state, and
β determines the response in shear, i.e. the evolution of the combined damage function in states where both damage functions are active.
To define the tensile damage evolution law dt(κ) (
Ref. 3), it is possible to use either
Linear strain softening,
Exponential strain softening, or the
Mazars damage evolution function, which is obtained by a combination of linear and exponential strain softening
(3-73)
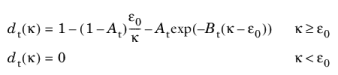
Here, At and
Bt are tensile damage evolution parameters, and
ε0t is the tensile strain threshold.
The compressive damage evolution law dc(κ) is obtained by the
Mazars damage evolution function
(3-74)
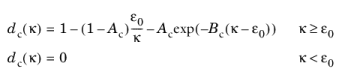
Here, Ac and
Bc are compressive damage evolution parameters, and
ε0c is the compressive strain threshold. Both the tensile and compressive damage evolution laws can also be specified by
User defined expressions.
This simplest regularization technique is based on stress-strain curves (damage evolution laws) that depend on the mesh and element characteristics. The method is often called the Crack Band method (
Ref. 4,
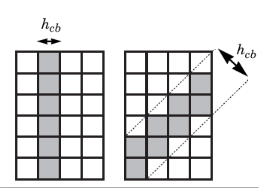
Ref. 5). The method regularizes the solution from a global viewpoint, which dissipates the correct amount of energy during strain localization. The main difficulty in using the crack band method is to find the correct width of the crack band,
hcb, which can depend on the element size and shape as well as the order of the interpolation and the current stress state (i.e. inclination of the crack with respect to the mesh).
|
•
|
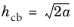 , for 2D triangles , for 2D triangles |
|
•
|
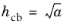 , for 2D rectangles , for 2D rectangles |
|
•
|
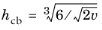 , for 3D tetrahedra , for 3D tetrahedra |
|
•
|
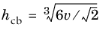 , for 3D pyramids , for 3D pyramids |
|
•
|
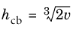 , for 3D wedges , for 3D wedges |
|
•
|
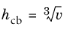 , for 3D hexahedra , for 3D hexahedra |
The crack band width hcb is then used to modify the
Damage evolution law in which the damage variable
d(κ) is computed. Note that the damage evolution laws (
Equation 3-73 and
Equation 3-74) are unaffected by the crack band method.
The Implicit Gradient method (
Ref. 6) enforces a predefined width of the damage zone through a localization limiter. This is achieved by adding a nonlocal strain variable, the
nonlocal equivalent strain εnl, through an additional PDE where the equivalent strain
εeq acts as source term. This PDE is solved simultaneously with the displacement field:
(3-75)
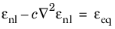
Here, the parameter c controls the width of the localization band. This parameter is defined from the Internal length scale lint, and the geometry dimension
n (two or three dimension)
(3-76)
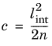
The strain-based formulation for the damage model (Equation 3-62) is then redefined by the nonlocal equivalent strain
εnl instead of the equivalent strain
εeq
(3-77)
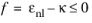
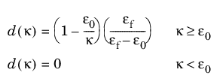 ,
,