Performing a Response Spectrum Analysis

Response spectrum analysis is used to approximately determine the structural response to short nondeterministic events like earthquakes and shocks. The idea is that the event is characterized by the peak response that it would give a single degree of freedom (SDOF) oscillator having a certain natural frequency and relative damping. The response value is provided as a function of the natural frequency of the oscillator.

If the dynamic structural response is viewed as a modal superposition, each eigenmode within the given frequency range acts as an SDOF oscillator, with a peak amplitude which is known from the spectrum. There is, however, no information about when each mode reaches it peak value. The most conservative assumption is that all modes should be combined using the individual peak values. Using such approach will in most cases result into an extremely conservative design. For this reason, other summation methods have been developed. When performing a response spectrum analysis, you will have access to several such methods.

Setting up a Response Spectrum Analysis

The response spectrum analysis is not a study type. The computations are performed during result evaluation. You enter the methods and parameters in the settings for the or data sets. These data sets require the following:

•

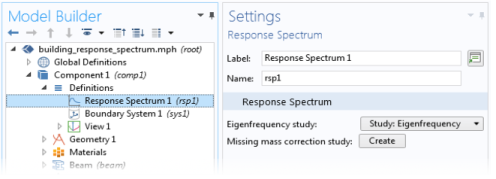
An eigenfrequency solution, where the eigenmodes to be included in the response spectrum analysis have been computed. All computed eigenmodes are used. If you want to filter out a particular set of modes, you can add a study step after the study step. Such a filter can for example be based on the effective modal mass, so that only modes which contribute significantly to the mass are included.


	The time to evaluate a result when using a response spectrum data set varies almost quadratically with the number of eigenmodes you include.

•

A corresponding set of modal participation factors. To generate them, add a node under in the component. If you have computed the eigenfrequency prior to adding the node, you need to perform an .

•

In some response spectrum evaluation methods, you are required to compensate for the mass which is not represented by the included eigenmodes. In order to do so, a number of special stationary load cases must also be computed. You can set up all nodes required in the model builder tree by clicking the : button in the node.

Adding a Response Spectrum Study

In the dialog, there is a study type called . When you select it, two things happen:

•

A study, containing a single study step is created.

•

A node is added under in the first component which contains at least one structural mechanics physics interface. In this node, the list will be initialized to point to the study step that was just created.

If you already have computed the eigenfrequencies of a structure, and then want to perform a response spectrum evaluation, there is no need to add a new study. Just add a node under , and then do an to make the new variables available.

Missing mass correction

You create a missing mass correction study from the node by clicking the : button.


	It is not possible to undo this operation. To revert, you will have to manually delete all the nodes which were created.

A number of items are then created in the model tree:

•

A set of load group nodes are created under There are two load groups for each spatial direction. The load group nodes are placed under a common group named .

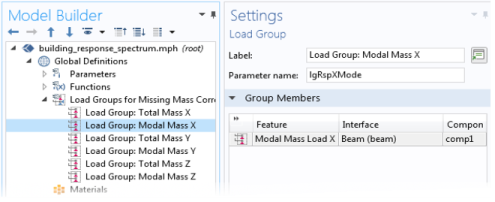The of the load group is reserved, and you should not modify it.

•

A new study named is created. This study contains three or four study steps, depending on the spatial dimension. First, there is one study step for each spatial direction. In these steps, a weighted sum of the eigenmodes is computed. The weights are the modal participation factors in each direction. This gives a measure of the mass that the eigenmodes represent.
These study steps must reference the eigenvalue solution, including any subsequent filtering. If you change the study from which the eigenmodes are to be taken, you must also change the choice in the drop-down in all of the nodes.The final study step in the study is a stationary study step, where each load group is solved separately by adding one load case per load group.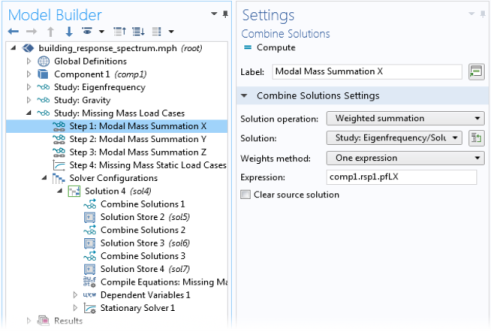

If the physics interface has loads other than those automatically generated for missing mass correction, you need to make sure that those loads are not solved for in the study step. There are several ways of doing that. You can, for example:

•

Disable the other load nodes temporarily in the model tree before solving.

•

Disable them in this study, by using in the section in the settings for the study step. This is the preferred method.

•

Assign the other loads to a new load group.

•

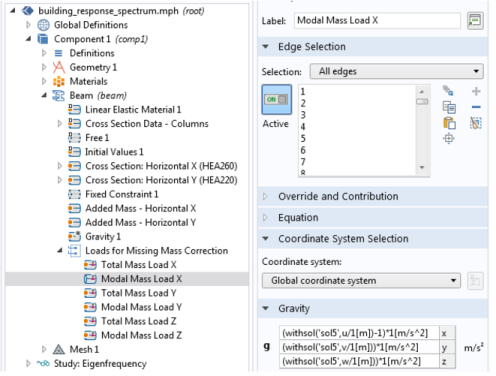
In each structural mechanics physics interface in the component, a set of nodes are added. There are two such nodes for each spatial direction. Each gravity node is connected to a corresponding load group. Half of the loads are pure gravity loads, used when only together with the . The other set of loads, which are used in the , are referencing the combined solutions as the depend on the computed eigenmodes. The gravity nodes are placed under a common group, named .

Settings for the Response Spectrum Data Sets

Defining the Spectra

You input the spectra as functions under . Usually, either an interpolation function, or an analytic function, or a piecewise function is used.

There are two common methods to describe the design response spectra: either as function of frequency, or as function of period time. Use the setting to control this.

The handling of units in the functions are nonstandard:

•

The unit of the argument is ignored. The function is called with either frequency (Hertz) or period time (seconds) as defined by the setting in .

•

The unit of the function is not checked. The function will however be scaled to model units, so if you for example enter the unit mm/s^2 for an acceleration spectrum, the function will (in an SI system) be scaled by 1/1000. You would get the same effect if the entered unit an inconsistent, for example mm.

The spectra you enter have the following correlation to the spatial directions:

•

In 2D, you give two spectra, one horizontal, and one vertical. The horizontal spectrum acts along the global X-axis, and the vertical one acts along the Y-axis.

•

In 3D, the vertical spectrum always acts along the global Z-axis.

•

In 3D, you can supply two different horizontal spectra, called primary and secondary horizontal spectrum respectively. Those spectra act in two orthogonal directions which by default coincide with the global X and Y directions. By giving a non-zero value to , you can make the primary spectrum act in an arbitrary direction in the X-Y plane.

•

Some methods in 3D (CQC3 and SRSS3) assume that the two horizontal spectra are equal except for an amplitude scale factor. In such case, you only provide one spectrum together with a (value between 0 and 1).

Mode Combination

The combination of the eigenmodes is the core of the response spectrum methods. Most commonly the combination is done in two passes: first the response to the excitation in each spatial direction is determined, and then a total response is computed by combining the spatial responses. However, for certain methods the total response is computed in one pass.

First, you select a method. If it is or , you also select a method.

The mode combination methods require different inputs. In particular, several of them provides a possibility to choose whether the coupling terms between modes are to be considered as always positive, or they may actually reduce the total response. This is controlled by the check box. Its default value differs between the methods, according to what is expected to be the most common choice.

Periodic Modes and Rigid Modes

For frequencies higher than the highest frequency content of the excitation, the SDOF system will respond as a rigid body. Some of the response spectrum evaluation methods take this into account. The effect is that high frequency (‘rigid’) modes are assumed to have a higher degree of correlation than low frequency (‘periodic’) modes. To take this effect into account, you can select to be the method or the method.

Missing Mass Correction

In general, only a small fraction of the total number of eigenmodes are used in the superposition. Therefore, some fraction of the total mass of the structure is not accounted for. The ignored modes usually have high natural frequencies. Such modes will not have a significant dynamic amplification. The mass in the corresponding SDOF system will just follow the movement of the foundation. This means that if the distribution of the missing mass is known, then it can be treated as an extra stationary mass force, where the peak acceleration during the event replaces the acceleration of gravity.

You can use two different methods for missing mass correction:

•

In the , the difference between the true mass distribution and the mass represented by the used eigenmodes will act as extra static load. Typically, most of the missing mass is located close to support points, where he modal amplitudes are low. This method can be used together with either the method or the method.

•

In the , the total inertial force is used as static load. At the same time, only the periodic part of the response is used in the mode summation. This method can only be used together with the method, since it is only compatible with the assumptions about how the rigid modes are scaled.

Result Interpretation

All results from a response spectrum analysis are positive; the evaluation methods contain absolute values or RMS-like operations. This has important implications for the interpretation of the results:

•

If the sign of your result quantity is important for the conclusions, you need to manually consider also the case of a negative value.

•

It is not meaningful to show deformation or vector plots of response spectrum results.

An underlying implicit assumption for response spectrum analysis is that it is performed in a frame of reference that follows the foundations of the structure. Thus, all displacements, velocities, and accelerations are relative to the foundation which in itself is accelerating. Thus, it is difficult to evaluate the absolute acceleration. The conservative way of doing so is to add the peak acceleration of the underlying event to the computed acceleration. This will usually be rather conservative since the peak of the excitation seldom coincides in time with the peak of the response.

For displacements, the relative displacements between two objects within the same moving frame is usually a more important result than the absolute displacement, so it does seldom matter whether a constant value is added to all points or not.