In the Settings window for the Geometrical Optics interface, select the Use corrections for strongly absorbing media check box in the physics interface
Intensity Computation section to modify Snell’s law and the Fresnel equations to accurately model refraction between media with complex refractive indices. This check box is available when
Intensity computation is set to
Compute intensity or
Compute intensity and power.
Following Chang et al. in Ref. 10, the wave vector in an absorbing medium is treated as a bivector with complex components,
where k is the wave vector,
k0 is the wave number in free space, and
e and
f are unit vectors with real-valued components indicating the normal direction to the surfaces of constant phase and surfaces of constant amplitude, respectively. The real-valued quantities
N and
K, sometimes called the apparent refractive indices, are related to the complex refractive index by the relations
where n − iκ is the complex refractive index of the medium. From these relations the apparent refractive indices can be computed as long as the dot product
e ⋅ f is known. To store information about the value of this dot product, auxiliary dependent variables for the components of
f are stored when the
Use corrections for strongly absorbing media check box is selected.
where θ and
ψ are the acute angles between the surface normal and the normal vectors to the surfaces of constant phase and surfaces of constant amplitude, respectively. The real part of the apparent refractive index in the second domain is a root of the quartic equation
where Ns = N1sin θ1,
Ks = K1sin ψ1, and the angle
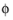
is the azimuthal angle between the normal to surfaces of constant amplitude and the plane of incidence. This equation is obviously quadratic in

and can thus be solved using the quadratic formula.