Radiation in Absorbing-Scattering Media Theory
The Radiation in Absorbing-Scattering Media Interface is available in 2D, 2D axisymmetric, and 3D components to model the propagation, attenuation, and scattering of an incident light within a semitransparent material considered to be non-emitting.
The radiative intensity I(Ω) at a given position following the Ω direction is the solution of the radiative transfer equation with no emission term (see Ref. 20):
(4-97)
where
•
κ, β, σs are absorption, extinction, and scattering coefficients, respectively (SI unit: 1/m) and are related by:
•
is the scattering phase function (SI unit: 1)
See Radiative Transfer Equation for details about the phase function, .
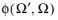
The incident radiation, denoted G, is defined by
If the Discrete Ordinates Method (DOM) is used for the approximation of Equation 4-97, G is computed as
and
where
•
Si is the i-th discrete ordinate.
•
Ii is the i-th component of the radiative intensity.
•
ωj is the i-th quadrature weight.
If the P1 Approximation Theory is used instead, G is the solution of the following equation
(4-98)
with the following boundary condition
where DP1 is the P1 diffusion coefficient.