In Figure 4-6, consider a point P located on a semi-transparent surface that has an emissivity εu, diffuse reflectivity ρd,u, specular reflectivity ρs,u, absorptivity αu, refractive index nu, and temperature Tu on the upside, and an emissivity εd, diffuse reflectivity ρd,d, specular reflectivity ρs,d, absorptivity αd, refractive index nd, and temperature Td on the downside. As the surface is assumed semi-transparent, some radiation is transmitted through the body.

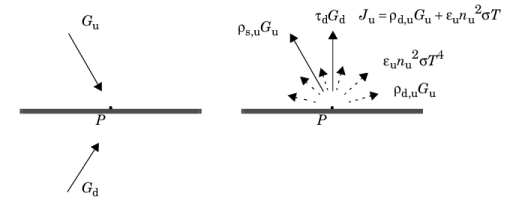
The total incoming radiative flux at P is called irradiation, and is denoted Gu on the upside and Gd on the downside. The total outgoing radiative flux at P is called radiosity and denoted Ju on the upside and Jd on the downside. This radiosity is the sum of diffusively reflected radiation, emitted radiation and transmitted radiation coming from the other side of the semi-transparent layer:

The net inward radiative heat fluxes on the upside and downside, qu and qd, are then given by the difference between the irradiation and the radiosity:

Bodies are considered to behave as ideal gray bodies, meaning that the absorptivity and emissivity are equal, and the reflectivity ρs is therefore obtained from the following relation:

Using Equation 4-72 to Equation 4-77, Ju and Jd can be eliminated and a general expression is obtained for the net inward heat fluxes into the semi-transparent body based on Gu, Gd, Tu and Td:

Thus, for ideal gray bodies, q is given by: