Particle Tracing with Mass
Use a Particle Tracing with Mass plot in 2D () or 3D () to visualize the trajectory of a particle with mass and subject to a flow field. Add a Color Expression or Deformation as needed. Right-click a 2D Plot Group or 3D Plot Group to add these plot types from the More Plots submenu.
For particles with mass, COMSOL Multiphysics generates the pathlines by solving the fundamental equation of motion:
for the pathline x ( t ). Here, m is the particle’s mass, F equals the force acting upon the particle, and t is time. This is a system of ODEs for x, which COMSOL Multiphysics solves using a pair of Runge-Kutta methods of orders four and five. The solver advances the algorithm with the solution of order five and uses the difference between the order-five and order-four solutions to obtain the local error estimate.
For massless particles, the equation of motion is:
The true formulation of Newton’s second law of motion is
That is, the time derivative of the mass must be considered. The particle-tracing algorithm does not solve this equation. Thus, if an expression is specified for the particle mass that depends on time, the result are incorrect.
Axisymmetric Models
In 2D axisymmetry, three components for the force are available for particles with mass.
When specifying all three, the algorithm solves for a line in 3D in cylindrical coordinates, but the plot only shows the projection on the axisymmetry plane. In this case, the centripetal force is considered; that is, the algorithm solves the equation
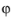
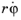
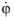
where m is the particle mass and (r, , z) are the cylindrical coordinates. The variable corresponding to the velocity component in the ϕ direction (the default name is partv) has the dimension length/time, and equals as has the dimension radians/time.
•
Go to Common Results Node Settings for links to information about these sections: Data, Title, Coloring and Style, Quality (Resolution and Recover only), and Inherit Style. For Particle Tracing with Mass plots, only Solution data sets are allowed as inputs.
•
See Particle Tracing for Particle Positioning, Release, Quality (ODE solver settings), and Advanced settings.
See Particle Tracing in Fluid Flow for more information about predefined expressions for drag-driven particle movement that are available for these models.
There is an additional setting under Coloring and Style for this plot.
The Type of Point Style available includes Comet tail. Comet tail plots provide a convenient way to indicate the direction of travel of particles at a given point in time. The tail of the comet typically points in the opposite direction to the particle velocity — so visually, it is the same as the tail of a comet approaching the sun. Go to Common Results Node Settings for the Comet tail settings links.
This plot type is intended for visualizing a small number of particles on simple geometries. The Particle Tracing Module has superior particle tracing capabilities and should be used for all but the simplest of models.
Total Force
Specify the total force acting on the particles. Click the Replace Expression () or Insert Expression () button to select predefined expressions based on the physics of the model. Or enter an Expression — for 2D, enter or select Fx and Fy components of the force; for 3D, enter or select Fx, Fy, and Fz components of the force. Enter a Description (or edit the default). When some predefined forces are added, there are additional Parameters with a Value to enter into a table.
Mass and Velocity
Enter the particle Mass. Enter the Initial velocity — for 2D enter values for the x component and y component; for 3D enter values for x component, y component, and z component.
Quality (ODE solver Settings)
Under Quality, also define the ODE solver settings as needed and described for Particle Tracing. Go to ODE Solver Settings — Relative Tolerance, ODE Solver Settings — Absolute Tolerance, and ODE Solver Settings — Step Size for details.
Advanced
Under Advanced, define the Particle velocity variables. Edit the default variable component names for each particle’s velocity. The default names are partu (x component), partv (y component), and partw (z component).
Under Advanced, also define these settings as needed and described for Particle Tracing. Go to Advanced — Termination and Advanced — Instantaneous Flow Field for details.