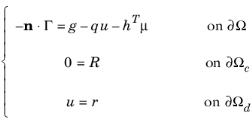Specifying and Interpreting Boundary Conditions

The formulation of the boundary conditions in general form (Equation 16-1) and coefficient form (Equation 16-2) imposes both Dirichlet and Neumann conditions at the same time:

where Γ is the flux vector (Γ = −c∇u−αu+γ for a coefficient form equation) and δΩc and δΩd are parts of the overall boundary, δΩ, where general constraints and Dirichlet conditions have been specified. Combining conditions of different types on the same boundary is possible because of a new dependent variable μ, which is defined only on the boundary. This unknown variable μ is called a Lagrange multiplier and usually has a physical interpretation. For example, in structural mechanics problems, the Lagrange multiplier equals the reaction forces on the boundary.

The factor hT in the Neumann boundary condition is the constraint force Jacobian. It decides how the Lagrange multipliers enforcing the constraint are scaled and distributed over the equations. The default settings in a Constraint node use

while a Dirichlet Boundary Condition node by default corresponds to hT = −1. For example:

•

The Dirichlet condition is u = r and the default constraint settings imply hT = −1. The Neumann condition becomes:

The Lagrange multiplier, μ, adjusts so as to satisfy the requested Dirichlet condition. Specifying a nonzero g changes the value of the Lagrange multiplier on the same boundary but does not affect the actual solution u. Therefore, this equation can usually be ignored, leaving effectively a pure Dirichlet condition.

•

When no constraint is applied on a boundary, the value of R is zero, or equivalently, the Dirichlet condition reads 0 = 0. Therefore hT is zero and the Neumann condition is:

The following example demonstrates a number of possible boundary condition combinations for a stationary system with two dependent variables u1 and u2 and two constraints when reaction terms are applied symmetrically on all physics. This is the default, and most useful, implementation. Written in general form:

with the default Neumann boundary conditions

writing out the symmetric application of reaction terms on all dependent variables, and the Dirichlet boundary conditions:

The same set of boundary conditions are accessible in all PDE interfaces. To illustrate the flexibility of the Constraint boundary condition R = 0, consider these cases:

Let R1 = R2 = 0. Then the Dirichlet boundary conditions give 0 = 0. In addition, the terms containing the Lagrange multipliers disappear from the Neumann boundary condition. Thus you have only the Neumann boundary conditions:

Let R1 = r1 − u1 and R2 = r2 − u2. Then the Dirichlet conditions are the usual u1 = r1 and u2 = r2. Using default settings for the constraint reaction terms,

and the Neumann boundary conditions become:

These last equations impose no restrictions on u1 or u2, because the Lagrange multipliers μ1 and μ2 always adjust so as to fulfill the Dirichlet conditions. In this case, ignore the Neumann boundary conditions.

Let R1 = r1 − u1 and R2 = 0. Then the Dirichlet conditions are

and the default Neumann conditions including reaction terms are:

The first Neumann condition can be ignored because it imposes no restriction on u1 or u2. You effectively have only the Dirichlet condition on u1 together with the second Neumann condition.

The same as Case 3 but with the two PDEs interchanged (Γ1 and Γ2 as well as F1 and F2). Then the PDEs are:

The Dirichlet condition is similar to that in Case 3: u1 = r1. By default, the Neumann conditions then become:

Effectively, you have only the Neumann condition −n · Γ1 = G1. In comparison with Case 3, the PDEs and the Dirichlet conditions are identical, while the Neumann conditions are different. Both the Dirichlet and the Neumann conditions are now applied on u1, and nothing is specified for u2.

	This example shows that when mixing Dirichlet and Neumann conditions on Coefficient Form PDEs and General Form PDEs, the ordering of the equations and the dependent variables are important. However, the ordering of the Dirichlet conditions does not matter because the different Lagrange multipliers are for all practical purposes indistinguishable from each other.

Finally, let R1 = u2 − u1 and R2 = 0. Also, assume that u1 and u2 exist on two adjacent domains rather than on the same domain. The normal vectors as seen from the two sides are then n1 = −n2 = n. Then the Dirichlet conditions are:

and the Neumann conditions using the default symmetric reaction terms are:

The same Lagrange multiplier now appears in both Neumann conditions, which can have different definitions of Γ and G. Therefore, contrary to Cases 2 and 3, the Neumann conditions cannot be ignored. Instead, adding the two conditions, it becomes apparent that the solution and flux on the boundary must fulfill:

In particular, if G1 = G2 = 0, the last condition simplifies to:

This means that both the variables u1 and u2 and the corresponding fluxes are equal at the boundary. If u1 and u2 represent the same quantity, this is the same continuity condition that holds implicitly at every mesh element boundary in the model, where nothing else has been specified.