where v is the velocity vector in the rotating coordinate system,
r is the position vector, and
Ω is the angular velocity vector. The relation between
v and the velocity vector in the stationary coordinate system is
The Rotating Machinery, Fluid Flow interfaces solve Equation 3-162 and
Equation 3-163, but reformulated in terms of a nonrotating coordinate system; that is, they solve for
u. This is achieved by invoking the
Arbitrary Lagrangian-Eulerian Formulation (ALE) machinery. In rotating domains,
x = x(Ω, t) as prescribed in the Rotating Domain under Definitions. The Navier-Stokes equations on rotating domains then read
The derivative operator 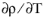 is the mesh time derivative of the density and appears in the equation view as d(rmspf.rho,TIME)
is the mesh time derivative of the density and appears in the equation view as d(rmspf.rho,TIME). Analogously,
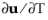
is the mesh time derivative of the velocity. The variable
TIME replaces
t as the variable for time.
The user input for a rotating domain prescribes the angular frequency, w. To calculate
Ω, the physics interfaces set up an ODE variable for the angular displacement
ω. The equation for
ω is
Ω, is defined as
w times the normalized axis of rotation. In 2D, the axis of rotation is the
z direction while it in 3D is specified in the Rotating Domain features. If the model contains several rotating domains, each domain has its own angular displacement ODE variable.