For the v2-f model, the turbulent viscosity is based on the velocity fluctuations, , normal to the streamlines. This makes it possible to model turbulence anisotropy, and to separate between low-Reynolds number effects and wall blockage. Nonlocal effects of the pressure fluctuations on the turbulent fields are included by applying elliptic relaxation to the pressure strain term (Ref. 26, Ref. 27). The formulation implemented in COMSOL Multiphysics, solves for the normalized velocity fluctuations,

and an elliptic blending function, α, which is used to combine near-wall effects with those in the far-field. The complete model for compressible flow reads,

where . The modified coefficients in the ε-equation are given by

Realizability Constraints are applied to the turbulent viscosity.

The wall distance variable, lw, is provided by a mathematical Wall Distance interface that is included when using the v2-f model. The solution to the wall distance equation is controlled using the parameter lref. The distance to objects larger than lref is represented accurately, while objects smaller than lref are effectively diminished by appearing to be farther away than they actually are. This is a desirable feature in turbulence modeling since small objects would get too large an impact on the solution if the wall distance were measured exactly.

The most convenient way to handle the wall distance variable is to solve for it in a separate study step. A Wall Distance Initialization study type is provided for this purpose and should be added before the actual Stationary or Time Dependent study step.

The automatic wall treatment is a way to obtain an accurate low-Reynolds-number formulation when the mesh allows it, and to fall back on a wall function formulation when the mesh is coarse. It is a blending between the solutions in the linear sublayer and the logarithmic layer respectively. A formulation for ω-based methods was described by Menter et al. in Ref. 9. The v2-f model uses a similar formulation and defines

δw is the distance to the closest wall. The boundary conditions for the momentum equations are a no-penetration condition u ⋅ n = 0 and a shear stress condition

In Equation 3-140, u+ = U||/uτ with

Here, κv, is the von Kárman constant (default value 0.41), U|| is the velocity parallel to the wall and B is a constant that by default is set to 5.2.

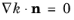
These expression can be combined with the lift-off concept shown in Figure 3-7 which gives δw = hw/2. The k-equation formally fulfills both at the wall and in the log-layer, so this condition is applied for all δw+.

The conditions for the turbulent dissipation rate, ε, is similar to that in the Wolfshtein model which is commonly employed in two-layer k-ε implementations (Ref. 13):

The boundary conditions applied on ζ and α are given by

The resulting wall resolution, δw+, is available as the postprocessing variable. Delta_wPlus.

The no slip condition, that is u=0 is applied when Wall Treatment is set to Low Re.

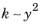
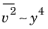
Since all velocities must disappear on the wall, so must k and ζ (since and ). Hence, k=0 and ζ=0 on the wall. By definition, α=0 on the wall.

The correct wall boundary condition for ε is

where n is the wall normal direction. This condition is however numerically very unstable. Therefore, ε is not solved for in the cells adjacent to a solid wall and instead the analytical relation

is prescribed in those cells (using the variable εw, which only exists in those cells). Equation 3-130 can be derived as the first term in a series expansion of

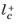is the distance, measured in viscous units, from the wall to the center of the wall adjacent cell. The boundary variable Distance to cell center in viscous units, lplus_cc, is available to ensure that the mesh is fine enough. Observe that it is unlikely that a solution is obtained at all if

The guidelines given in Inlet Values for the Turbulence Length Scale and Turbulent Intensity for selecting the turbulence length scale, LT, and the turbulence intensity, IT, apply also to the v2-f model.

The v2-f model has the same default initial guess as the standard k-ε model (see Initial Values) but with replaced by lref. The default initial values for ζ and α are 2/3 and 1 respectively.

The default initial value for the wall distance equation (which solves for the reciprocal wall distance) is 2/lref.

In some cases, especially for stationary solutions, a fast way to convergence is to first solve the model using the ordinary k-ε model and then to use that solution as an initial guess for the v2-f model. The procedure is then as follows:

The v2-f model applies absolute scales of the same type as the k-ε model (see Scaling for Time-Dependent Simulations).