You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The k-
ω model solves for the turbulent kinetic energy,
k, and for the dissipation per unit turbulent kinetic energy,
ω.
ω is also commonly know as the specific dissipation rate. The CFD Module has the Wilcox revised
k-
ω model (
Ref. 1)
(3-92)
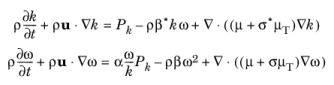
(3-93)
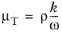
(3-94)
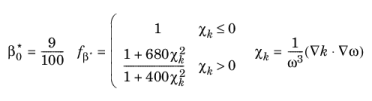
where in turn Ωij is the mean rotation-rate tensor
and Sij is the mean strain-rate tensor
Pk is given by
Equation 3-76. The following auxiliary relations for the dissipation,
ε, and the turbulent mixing length,
l∗, are also used:
(3-95)
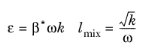
The implementation of the k-
ω model relies on the same concepts as the
k-
ε model (
Ref. 10). This means that the following approximations have been used:
where lr is the limit given by the realizability constraints (
Equation 3-81 and
Equation 3-82).
(3-96)

(3-97)
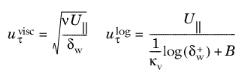
where δw is the distance to the nearest wall,
κv, is the von Kárman constant (default value 0.41),
U|| is the velocity parallel to the wall and
B is a constant that by default is set to 5.2. Menter et al. (
Ref. 9) suggested the following smooth blending expressions for
ω and
uτ:
(3-98)
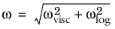
(3-99)
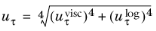
These expression can be combined with the lift-off concept shown in Figure 3-7 which gives
δw = hw/2. The wall condition for
ω is given by
Equation 3-98 and the conditions for the momentum equations are a no-penetration condition
u ⋅ n = 0 and a shear stress condition
(3-100)
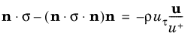
The k-equation formally fulfills

both at the wall and in the log-layer, so this condition is applied for all
δw+.
The system given byEquation 3-83 through
Equation 3-100 are, however, nonlinear in
uτ and not very stable. To circumvent this, a variable
u∗, log is introduced (see
Ref. 10 and
Ref. 11) such that
(3-101)
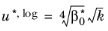
(3-102)
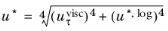
Equation 3-102 is in turn is used to calculate an alternative dimensionless wall distance
(3-103)

Equation 3-102 is used instead of
uτ in the expression for
ωlog and
Equation 3-103 is used instead of
δw+ in the expression for
uτlog. The traction condition in
Equation 3-100 is replaced by
(3-104)

The resulting wall resolution, δw+, is available as the postprocessing variable
Delta_wPlus.
When Wall Treatment is set to Wall functions, wall boundaries are treated with the same type of boundary conditions as for the
k-
ε model (see
Wall Functions) with
Cμ replaced by
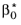
and the boundary condition for
ω given by
(3-105)
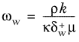
The k-
ω turbulence model can be integrated all the way down to the wall and is consistent with the no-slip condition
u = 0. Since all velocities must disappear on the wall, so must
k. Hence,
k=0 on the wall.
(3-106)
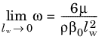
To avoid the singularity at the wall, ω is not solved for in the cells adjacent to a solid wall. Instead, its value is prescribed by
Equation 3-106 (using the variable
ωw, which only exists in those cells). Accurate solutions in the near-wall region require that,
(3-107)

where uτ is the friction velocity which is calculated from the wall shear-stress
τw,
(3-108)
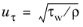
The boundary variable Distance to cell center in viscous units,
lplus_cc, is available to ensure that the mesh is fine enough. According to
Equation 3-107,
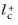
should be about
0.5. Observe that very small values of
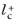
can reduce the convergence rate.
Since the ωw requires the wall distance, a wall distance equation must be solved prior to solving a
k-
ω model with low-Reynolds-number wall treatment.
The k-
ω model applies absolute scales of the same type as the
k-
ε model (see
Scaling for Time-Dependent Simulations) except that the scale for
ω is given by
The k-
ω model can in many cases give results that are superior to those obtained with the
k-
ε model (
Ref. 1). It behaves, for example, much better for flat plate flows with adverse or favorable pressure gradients. However, there are two main drawbacks. The first is that the
k-
ω model can display a relatively strong sensitivity to free stream inlet values of
ω. The other is that the
k-
ω model is numerically less robust than the
k-
ε model.