where μ is the dynamic viscosity,
ρ the density, and
U and
L are velocity and length scales of the flow, respectively. Flows with high Reynolds numbers tend to become turbulent. Most engineering applications belong to this category of flows.
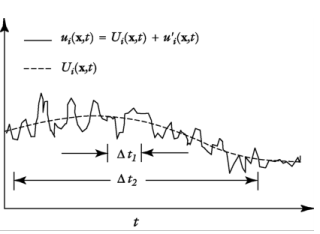
where  can represent any scalar quantity of the flow. In general, the mean value can vary in space and time. This is exemplified in Figure 3-6
can represent any scalar quantity of the flow. In general, the mean value can vary in space and time. This is exemplified in Figure 3-6, which shows time averaging of one component of the velocity vector for nonstationary turbulence. The unfiltered flow has a time scale
Δt1. After a time filter with width
Δt2 >> Δt1 has been applied, there is a fluctuating part,
u′i, and an average part,
Ui. Because the flow field also varies on a time scale longer than
Δt2,
Ui is still time-dependent but is much smoother than the unfiltered velocity
ui.
where U is the averaged velocity field and
⊗ is the outer vector product. A comparison with
Equation 3-59 indicates that the only difference is the appearance of the last term on the left-hand side of
Equation 3-60. This term represents the interaction between the fluctuating parts of the velocity field and is called the Reynolds stress tensor. This means that to obtain the mean flow characteristics, information about the small-scale structure of the flow is needed. In this case, that information is the correlation between fluctuations in all three directions.
where μT is the
eddy viscosity, also known as the turbulent viscosity. The spherical part can be written
where k is the turbulent kinetic energy. In simulations of incompressible flows, this term is included in the pressure, but when the absolute pressure level is of importance (in compressible flows, for example) this term must be explicitly included.
and a variable, ui, is decomposed into a mass-averaged component,

, and a fluctuating component,
ui″, according to
Using Equation 3-62 and
Equation 3-63 along with some modeling assumptions for compressible flows (
Ref. 7),
Equation 3-14 and
Equation 3-15 can be written on the form
where k is the turbulent kinetic energy. Comparing
Equation 3-64 to its incompressible counterpart (
Equation 3-60), it can be seen that except for the term
