Fully Developed Flow (Inlet)
The Fully Developed Flow boundary condition can be understood from the following figure:
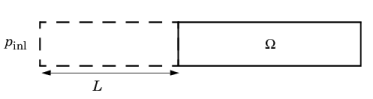
The flow to the domain Ω is assumed to enter through a straight channel of length L. The channel is a virtual extrusion of the inlet cross section and a pressure constant pressure Pinl is applied on the inlet of the virtual channel.
The Fully Developed Flow boundary condition prescribes that the tangential flow component on the boundary is zero:
The momentum equation for a fully developed flow in the virtual extrusion of the inlet cross section can then be projected onto the inlet boundary with the following weak equation as the result:
The exact value of L is somewhat arbitrary as long as it is not too high or too low. L is therefore set to ten times the inlet edge length in 2D and to ten times the square root of the inlet area in 2D axisymmetry and in 3D.
The fact that the velocity profile is not prescribed, but rather the solution of a projected weak contribution, means that the actual velocity profile that is obtained on the inlet can deviate from the analytical fully developed flow profile (in cases such an analytical solution exists) if required by the solution inside the computational domain, Ω. This is most notably if the flow is strongly curved just downstream of the inlet. This can for example be the case if an object is positioned just downstream of the inlet or if the adjacent boundaries are not orthogonal to the inlet. The analytical solution can in these cases be recovered by including a little bit of the inlet channel in the computational domain.
The inlet pressure, Pinl, must be solved for and the its equation is a discrete algebraic equation (DAE) for Pinl. When, for example, the average velocity is specified, the DAE reads
where <⋅> denotes the average over the inlet. Since the equation for Pinl is a DAE (the equation for Pinl does not contain Pinl), it must be solved coupled to Navier-Stokes and it must be treated by a Vanka pre- and post-smoother if iterative solvers are employed.
The boundary conditions for the virtual inlet channel are inherited from the boundaries adjacent to the inlet channel. Virtual boundaries adjacent to walls (except slip walls) are treated as no-slip walls. Virtual boundaries adjacent to any other type of boundary are treated as slip-walls (or equivalently as symmetry boundaries). So in the figure above, if the lower boundary of Ω is a no-slip wall and the top boundary is a symmetry boundary, the lower boundary of the virtually extruded channel becomes a no-slip wall and the upper boundary a symmetry boundary.
Algebraic turbulence models need to additional equations or constraints. For all other turbulence models, their weak equations in the virtual inlet channel are projected onto the inlet of the computational domain. The projections are regularized to prevent the production to fall to zero, so the solutions of the projects can show slight deviation from the correct solutions close to no-slip walls.