Equations for compressible turbulence are derived using the Favre average. The Favre average of a variable T is denoted and is defined by

With this notation the equation for total internal energy, e, becomes

where h is the enthalpy. The vector

is the laminar, viscous stress tensor. Notice that the thermal conductivity is denoted λ.

is modeled using the Boussinesq approximation:

where k is the turbulent kinetic energy, which in turn is defined by

The correlation between 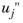and 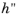in Equation 4-3 is the turbulent transport of heat. It is modeled analogously to the laminar conductive heat flux

are modeled by a generalization of the molecular diffusion and turbulent transport terms found in the incompressible k equation

Inserting Equation 4-4, Equation 4-5, Equation 4-6, Equation 4-7 and Equation 4-8 into Equation 4-3 gives

The Favre average can also be applied to the momentum equation, which, using Equation 4-5, can be written

Taking the inner product between 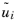and Equation 4-10 results in an equation for the resolved kinetic energy, which can be subtracted from Equation 4-9 with the following result:

According to Wilcox (Ref. 1), it is usually a good approximation to neglect the contributions of k for flows with Mach numbers up to the supersonic range. This gives the following approximation of Equation 4-11 is

Larsson (Ref. 2) suggests to make the split

Equation 4-13 is completely analogous to the laminar energy equation and can be expanded using the same theory (see for example Ref. 3):

This is a relatively exact model for PrT, while still quite simple. In Ref. 4, it is compared to other models for PrT and found to be a good approximation for most kinds of turbulent wall bounded flows except for turbulent flow of liquid metals. The model is given by

where the Prandtl number at infinity is PrT∞ = 0.85 and λ is the conductivity.

Weigand and others (Ref. 5) suggested an extension of Equation 4-14 to liquid metals by introducing

where Re∞, the Reynolds number at infinity must be provided either as a constant or as a function of the flow field. This is entered in the Model Inputs section of the Fluid feature.

Both automatic wall treatment and wall functions introduce a theoretical gap between the solid wall and the computational domain for the fluid and temperature fields. See Wall Boundary Conditions described for The Algebraic yPlus Turbulence Model and The k-ε Turbulence Model). This theoretical gap applies also to the temperature fields but is most often ignored when the computational geometry is drawn.

The heat flux between the fluid with temperature Tf and a wall with temperature Tw, is:

where ρ is the fluid density, Cp is the fluid heat capacity, u∗ is the friction velocity given by the wall treatment (u∗ for two-equation RANS models with automatic wall treatment and uτ for all other cases). T+ is the dimensionless temperature and is given by (Ref. 6):

λ is the thermal conductivity, and κ is the von Karman constant equal to 0.41.

The distance between the computational fluid domain and the wall, δw, is always hw/2 for automatic wall treatment where hw is the hight of the mesh cell adjacent to the wall. hw/2 is almost always very small compared to any geometrical quantity of interest, at least if a boundary layer mesh is used. For wall function, δw is at least hw/2 and can be bigger if necessary to keep δw+ higher than 11.06. So the computational results for wall functions should be checked so that the distance between the computational fluid domain and the wall, δw, is everywhere small compared to any geometrical quantity of interest. The distance δw is available for evaluation on boundaries.