Modeling Electrochemical Reactions
Electrochemical reactions are defined by using Electrode Reaction or Porous Electrode Reaction nodes. An electrode reaction is defined by its thermodynamics, kinetics, and stoichiometry. The latter describes the mass fluxes, sources and sinks arising due to a certain current density of the reaction.
Thermodynamics of Electrochemical Reactions
An electrolytic reaction involves the exchange of electrons with the electrode. Such a reaction is written as reduction, even if the reaction occurs predominantly in the oxidative direction. For example:
This reaction is called a “half-cell” reaction, since it will occur at a specific electrode-electrolyte interface. It cannot occur in isolation, but only when coupled to another half-cell reaction within a two-electrode electrochemical cell. Each reaction has a characteristic Gibbs energy change that determines whether or not it is thermodynamically favorable. A negative Gibbs energy change means that the reaction proceeds spontaneously — it is thermodynamically “downhill”.
The Gibbs energy change is related to the equilibrium potential difference from the electrode to the electrolyte according to:
where Eeq,m is the potential difference on some external reference scale for which the reaction is at equilibrium (ΔG = 0). This is called the equilibrium potential or reduction potential (or in corrosion, corrosion potential) of the electrochemical reaction, and its absolute value depends on the choice of reference electrode.
Equilibrium potentials should always be quoted versus a specific reference. If a different reference scale is used in different parts of your model, the thermodynamics of the system may not behave as expected.
From the standard thermodynamic relation
it follows
This is the Nernst equation which is a universal thermodynamic expression. It is always true of systems at thermodynamic equilibrium; it does not necessarily apply to systems not at equilibrium.
Assuming that the species are ideal and that activity effects can be treated as constant, then for the conversion between unimolecular reduced and oxidized species:
Hence at equilibrium, the concentrations of reactants and products at the electrolyte-electrode surface are related by an expression which depends on the potential difference between the two phases, and two reaction parameters: n, the number of electrons transferred per molecule reduced; and Ef, the formal reduction potential of the reaction measured on the same potential scale as the electrode-electrolyte potential difference.
The quantity
is known as the overpotential and is particular to a specific reaction occurring at the interface.
η depends on both the electric potential in the electrode φs and the electrolyte potential φl. Where there is substantial resistance to current flow through a solution, the corresponding potential difference in φl, called ohmic drop, alters the position of the electrochemical equilibrium. Additional applied potential in the electrical circuit may then be needed to drive an equivalent overpotential.
Kinetics of Electrochemical Reactions
The Nernst equation tells us the position of equilibrium of a reaction. However, it tells us nothing about how fast the system may get there. If there is a kinetic limitation — that is, if the reaction proceeds slowly — the equilibrium condition may never be observed. As a familiar example, diamond is thermodynamically unstable with respect to reacting to form graphite at room temperature and pressure. However, this reaction is kinetically limited by a vast activation energy for the reorientation of atoms, such that it is never in practice observed, and diamond is technically described as metastable.
We encounter the same issue in many electrochemical contexts. Reactions are prevented from proceeding to their equilibrium by kinetic limitations. Indeed, overcoming the natural kinetic sluggishness of the surface reactions of small, nonpolar molecules such as hydrogen and oxygen is key to much fuel cell research.
There are two important expressions describing the current density due to an electrochemical reaction as a function of the overpotential and the concentrations of reactant and product. It should be noted that the validity of these expression is not general and can never replace experimental kinetic data if such is available.
The first is the Tafel law which describes an irreversible anodic or cathodic process:
The constant A is the Tafel slope and has units 1/V. It is usually close to a half-integer multiple of F/RT and is less than or equal to nF/RT. Note that a reference exchange current density i0 must be specified for the reaction. This is by definition the current density drawn at zero overpotential.
The Tafel law assumes that a reaction is irreversible. If the reverse reaction might occur in practice, Tafel kinetics will not be correct.
The second expression is the Butler-Volmer equation which describes a reversible process, so that either anodic or cathodic current may flow depending on the sign and magnitude of the overpotential:
The Butler-Volmer equation is the most general description of electrode kinetics. It is highly adaptable because:
•
i0 is an empirical quantity.
•
It agrees with the Nernst equation when i = 0, so for a very fast reaction () then the Butler-Volmer equation gives the same potential difference as the Nernst equation. This is equally true under high resistance conditions.
•
It agrees with the Tafel equation when either the anodic or cathodic term dominates. For highly irreversible reactions (very low i0), appreciable current is only drawn for large overpotential, so this is typically the case.
For a discussion on the Butler-Volmer expression and concentration changes of the participating species, see the Defining Concentration Dependent Butler-Volmer Kinetics section below.
For a reversible reaction at very low overpotential (η of order RT/F ~ 25 mV), the exponentials in the Butler-Volmer equation can be linearized:
 
Using a linearized Butler-Volmer reaction can be advantageous when investigating convergence issues of a model.
The linearized Butler-Volmer equation is not correct for applied overpotentials larger than (RT / F). This is about 25 mV at room temperature. It is not suitable outside this range and therefore its use is confined to electrochemical processes occurring exclusively at low current density, such as electroplating or electrochemical impedance spectroscopy.
Electrode Kinetics Expressions
Fluxes and Sources/Sinks due to Electrode reactions
Electrode reactions will result in a molecular flux of reacting species to or from the electrode surface. If you are including mass transport in your model it is common to couple the flux of a reacting species on a boundary to the electrode reaction current density (by the Faraday’s law of electrolysis).
The coupling of chemical flux to electric current density is automated in some of the Electrochemistry interfaces by defining the reaction stoichiometry in the Electrode Reaction and Porous Electrode Reaction nodes. In the Chemical species transport interfaces the coupling however need to be set up manually by the Electrode Surface Couplingnodes. When modeling porous electrodes, the corresponding coupling node to create a source/sink a domain is the Porous Electrode Coupling node.
The mathematical treatment can be summed up by the expression:
This means that the flux Nj of chemical species j into the surface is proportional to the current density im due to reaction m drawn at an electrode-electrolyte interface. The constant of proportionality is the stoichiometric number for the species divided by n, the number of electrons transferred per mole of reactant, in a reductive direction and F the Faraday constant (96485 C/mol, the absolute charge on a mole of electrons).
As such, knowledge of the stoichiometry of an electrochemical reaction allows the local flux of a chemical species to be coupled to the current density contributed by that reaction. Note that multiple reactions may take place simultaneously at an electrode, and their contributions to the current density are simply summed.
The stoichiometric coefficients of the chemical species in an electrochemical reaction are conventionally written with the forward reaction in the direction of reduction, even if in practice within the system the reaction predominantly proceeds in the other direction.
COMSOL Multiphysics uses the standard convention that anodic (oxidative) current is positive. Cathodic (reductive) current is negative.
Defining Concentration Dependent Butler-Volmer Kinetics
If the concentrations at an electrode surface change, this will have an impact on the local kinetics. The Butler-Volmer kinetics expression is derived by considering the rate of a redox reaction
(2-1)
as the sum of the forward and backward rates according to:
(2-2)
where kfwd and krwd are reaction rate constants and cO and cR are the activities of the oxidized and reduced species of the redox couple, respectively. The potential E is here defined as
(2-3)
and the transfer coefficients are equal the sum of electrons in the charge transfer reaction according to
(2-4)
By defining an equilibrium potential at which the forward reaction and backward reaction rates are equal, Equation 2-1 can be shown to be equivalent to the commonly used Butler-Volmer equation:
(2-5)
In this formulation the exchange current density, i0, is defined as:
(2-6)
where i0,0 is the exchange current density at standard conditions.
The overpotential is here defined as
(2-7)
where Eeq is the equilibrium potential is defined by the Nernst equation as
(2-8)
and Eeq,0 is the equilibrium potential at standard conditions.
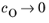
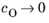
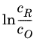
Note that in Equation 2-5 both i0 and Eeq are concentration dependent. This has some numerical drawbacks when modeling electrochemical cells including mass transport, since for low concentrations of the participating species (that is, when or ), the factor may get undefined during the solution process. An expression of the form of Equation 2-2 is more desirable since this expressions contains a simple linear dependence on the species activities.
A common solution to this issue is to rewrite the Butler-Volmer expression by defining the overpotential with respect to a fixed reference state for the activities cR, ref and cO, ref (typically corresponding to the inlet or initial concentrations), resulting in
(2-9)
where
(2-10)
and
(2-11)
with
(2-12)
Note that Equation 2-9 now contains a linear dependence on the activities cO and cR.