Ox and Red represent the oxidized and reduced forms of the chemical species, respectively.

The most general equation to describe the rate of this reaction as it proceeds at an electrode surface is the electroanalytical Butler–Volmer equation:

where k0 is the heterogeneous rate constant (SI unit: m/s) and αc is the (cathodic) transfer coefficient (dimensionless). For a one-electron reduction, the anodic and cathodic transfer coefficients are related as follows .

When the current is zero, the electroanalytical Butler–Volmer equation can be rearranged to the thermodynamic Nernst equation relating the equilibrium concentrations of the reacting species:

Where the flux of the reacting species is negligible compared to the concentration of these species, the concentrations are roughly constant (cRed ~ cOx ~ c). This converts Equation 4-14 into the Butler–Volmer equation written in terms of an exchange current density i0 (SI unit: A/m2):

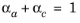
The exchange current density i0 (SI unit: A/m2) is then related to the heterogeneous rate constant as .
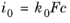