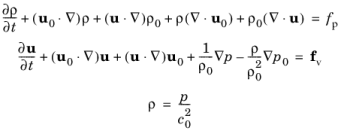Pierce argues for the use of the adiabatic assumption for the acoustic processes (perturbations in the entropy, s = 0) but also for not retaining the 0th order entropy variable
s0 (background mean flow entropy). The argument is that the entropy
s only varies because of variations in the background fields (it is zero in a homogeneous medium). This leads to a term in the momentum equation that is second order in gradients of the background field, for example,
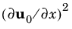
and so forth. These terms are disregarded. This also means that the equations are not valid when these terms are large, meaning when gradients in the background fields are large.
where U is the vector containing the dependent variables (
p,
u),
da is the mass matrix of the system,
Γ is the flux matrix, and
S is the right-hand-side (RHS) source vector. The conservative form of
Equation 6-1 is derived as follows. Start with Euler’s equations on a conservative form (omitting the RHS). For now, the dependent variables represent the full fields (not the acoustic perturbations). The continuity, momentum, and equation of state can be written
The equations describe the conservation of mass ρ and momentum flux
ρu. Linearize these equations according to the usual scheme, using
Now, insert these into Equation 6-3 and retain only 1st order terms (the acoustic perturbations)
Equation 6-4 can now be put on the form given in
Equation 6-2 yielding the following components
with u = [
u, v, w]
T and
u0 = [
u0, v0, w0]
T, and the flux components are