The viscous and thermal boundary layer thickness (thermal and viscous penetration depth) as defined in Theory Background for the Thermoviscous Acoustics Branch can be evaluated in postprocessing for the frequency domain models. The same is the case for the Prandtl number relating the two length scales (available in both frequency and time domain).

Material properties are readily available for postprocessing in plots. In plots click the Replace Expression icon and browse to the Material properties list under the thermoviscous acoustics interface. Important parameters to plot are the coefficient of thermal expansion phys_id.alpha0 and the isothermal compressibility phys_id.betaT. These should not evaluate to zero.

The stress tensor components are defined as variables and can be evaluated in postprocessing or used to create exotic couplings between physics. In the table below only the xx component of the stress tensor and the x component of the stress are shown. Change the spatial reference accordingly,

The energy conservation-dissipation corollary describes the transport and dissipation of energy in a system (see Ref. 1 p. 516 or Ref. 6). In linear acoustics, this equation is derived by taking the dot product (scalar product) of the momentum and the velocity v, adding it to the continuity equation, and then adding the entropy. After some manipulation and integration, the use of Gauss’ theorem yields Equation 5-1

where w is the disturbance energy of the control volume, u = |u| is the velocity, T is the temperature variation, p is the acoustic pressure variations, p0 is the background equilibrium pressure, T0 the background equilibrium temperature, ρ0 the background density, c0 the (isentropic) speed of sound, Cp the heat capacity at constant pressure (per unit mass), k the coefficient of thermal conduction, i is the instantaneous intensity (flux of energy out of a control volume), Δ is the dissipated energy per unit volume and time (SI unit: Pa/s = J/(m3s) = W/m3), s is the entropy, τ is the viscous stress tensor, 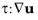is the viscous dissipation function, and T indicates transpose of vector. Δv and Δt are the viscous and thermal contributions to the dissipation function. In Equation 5-1 we have made use of Ref. 6 for the expression for the intensity I.

In the Thermoviscous Acoustics, Frequency Domain interface, the dissipation term Δ is directly given by the RMS value of the tensor expression

where “:” in Equation 5-2 is the double dot operator (or total inner product) and * is the complex conjugate. In the above expressions, the time averaged expressions for a product in the frequency domain is defined as:

The power dissipation variables are defined in Table 5-4.

In the Thermoviscous Acoustics, Frequency Domain interface the (time averaged) intensity I is given by averaging the instantaneous intensity vector i in Equation 5-1 using the same time averaged products defined above. The intensity and intensity magnitude are defined in Table 5-5.

In the Thermoviscous Acoustics, Transient interface the instantaneous intensity i variables is available for postprocessing. The instantaneous intensity and instantaneous intensity magnitude are defined in Table 5-6.

Several dedicated variables exist for The Thermoviscous Acoustics, Boundary Mode Interface where quantities are defined in terms of their in-plane and out-of-plane values. For example, the intensity variable I has the following derived values

where ip stands for in-plane and op for out-of-plane. These two variables are named tabm.Iip and tabm.Iop (with spatial components x, y, and z). The magnitude of these two variables is given by tabm.Iip_mag and tabm.Iop_mag. In the same manner variables exist for the acceleration and the velocity.