For the sake of brevity, consider the 1D Equation 2-53. In order to derive the PML formulation in the time domain, the following steps are taken (Ref. 39). First, consider a special form of the mapping Equation 2-52:

Then, taking Equation 2-54 into account, multiply Equation 2-53 by 1+σ(x)/iω. Equation 2-53 transforms to the following form:

The transformation to the time domain is performed according to the rule . Its direct application to Equation 2-55 would result in a time integral of p. To avoid this, an auxiliary variable u is introduced:

Equation 2-55 and Equation 2-56 yield a system of partial differential equations in the time domain equivalent to the frequency domain Equation 2-53:

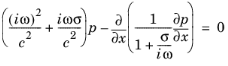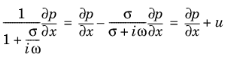The derivation of the model in 3D space, where more auxiliary variables are required, is given in Ref. 39.

In the axisymmetric cases, the coordinate stretching in PML domains is expressed in curvilinear coordinates. A thorough study of the use of PMLs for such problems in the frequency and the time domains is given in Ref. 40.