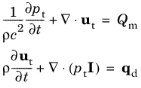The Pressure Acoustics, Time Explicit Model node adds the equations to model the transient propagation of linear acoustics waves based on the dG-FEM method. For the time explicit method used, the governing equations are formulated as a first order system, in terms of the linearized continuity equation and the linearized momentum equation, as

where pt is the total acoustic pressure, ut is the total acoustic velocity, ρ is the fluid density, and c is the speed of sound. Domain sources like a Mass Source, Heat Source, or Volume Force Source can be defined through the right hand sides Qm and qd. These two source terms represent the same quantities as the Monopole Domain Source and the Dipole Domain Source in The Pressure Acoustics, Frequency Domain Interface and The Pressure Acoustics, Transient Interface.

The dependent variables are the acoustic pressure p and the acoustic velocity u (sometimes called particle velocity or perturbation velocity). The equations are formulated in the total fields pt and ut which is the sum of the scattered field (the dependent variable solved for) and a possible background field pb and ub. The background field can be set up using the Background Acoustic Field feature.

The equations solved are the linearized Euler equations in a quiescent setting. The equations are easily combined to generate the scalar wave equation solved in The Pressure Acoustics, Transient Interface as discussed in Theory Background for the Pressure Acoustics Branch.

In the formulation of the wave equation, the speed of sound c and density ρ may in general be space dependent but only slowly varying in time, that is, at a time scale much slower than the variations in the acoustic signal.

In the Settings window, define the properties for the acoustics model and model inputs including temperature.

Select a Fluid model: Linear elastic (the default) or Ideal gas. If Linear elastic is selected enter the speed of sound c and the density ρ. If Ideal gas is selected enter the combination of material properties defining the gas. The default is to use the property values from the material (From material). Select User defined from the list to enter a user-defined value or expression in the text field that appears.

To display this section, click the Show button () and select Stabilization. In this section, you specify the value of the Lax-Friedrichs flux parameter τLF (default value: 0.2). This value controls the numerical flux between the elements (nodal discontinuous Lagrange elements) used with the discontinuous Galerkin (dG) method. The numerical flux defines how adjacent elements are connected and how continuous p and u are. Different definitions of the numerical flux lead to different variants of the dG method. The flux implemented here is the so-called global Lax-Friedrichs numerical flux. The value of the parameter τLF should be between 0 and 0.5. For τLF = 0 a so-called central flux is obtained. Setting τLF = 0.5 gives a maximally dissipative global Lax-Friedrichs flux.

To display this section, click the Show button () and select Advanced Physics Options. By default, the filter parameters α, ηc, and s are not active. Select the Activate check box to activate the filter. The filter provides higher-order smoothing for the dG formulation. Inside absorbing layers the settings given here are overridden by the Filter Parameters for Absorbing Layers.