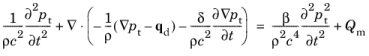Nonlinear Acoustics (Westervelt)
The propagation of finite-amplitude pressure waves cannot be described by the linear acoustic wave equation (small perturbation assumption) and requires solving the full nonlinear second-order wave equation. The latter allows a simplification when cumulative nonlinear effects dominate local nonlinear effects, for example, when the propagation distance is greater than the wavelength. The simplified equation is referred to as the Westervelt equation and reads
,
where δ is the diffusivity of sound and β is the coefficient of nonlinearity. In general the linear assumption is only valid when
which has a value of approximately 1.5·105 Pa for air and 2·109 Pa for water. So whenever the acoustic pressure is say a factor 100 less than these values the linear assumption holds. When this is not the case the Nonlinear Acoustics (Westervelt) model should be used.
The Nonlinear Acoustics (Westervelt) node adds the nonlinear contribution (first term on the right hand side) to the Transient Pressure Acoustics Model. That is, the linear acoustic wave equation transforms to the nonlinear Westervelt equation. To add the dissipation term (last term on the left hand side) select, for example, the General dissipation as the Fluid model in the Transient Pressure Acoustics Model.
The resulting equation is nonlinear and therefore does not allow the application of the superposition principle. In particular, the Background Pressure Field (for Transient Models) cannot be defined together with the Nonlinear Acoustics (Westervelt) feature.
The presence of the Nonlinear Acoustics (Westervelt) node changes the default solver settings for the proper treatment of nonlinearities. It is therefore required to Reset Solver to Defaults whenever the feature is added to or removed from the model.
The frequency spectrum of a nonlinear wave model contains not only the center frequency f0 but also the harmonics N·f0, N = 1,2,3,… generated. The Maximum frequency to resolve in the Transient Solver Settings section should be specified to resolve a desired number of harmonics to achieve a certain precision. This is especially important for shock waves, where the number of harmonics to resolve can exceed 10.
•
For the theory background of this nonlinear feature, see Pressure Acoustics, Transient Equations.
coefficient of nonlinearity
Specify the coefficient of nonlinearity. The available options are From parameter of nonlinearity (the default), From ratio of specific heats (for gases), and User defined.
•
For the option From parameter of nonlinearity enter the value of the Parameter of nonlinearity, B/A. The coefficient of nonlinearity is defined as follows
The parameter of nonlinearity quantifies the effect of nonlinearity on the local speed of sound in the fluid. It is expressed as c = c0 + (B/2A)u in the first order terms, where u is the acoustic particle velocity.
•
For the option From ratio of specific heats (for gases) enter the Ratio of specific heats, γ. This option is valid for perfect gases under isentropic conditions. Here,
B/A = γ - 1, which yields
•
Chose the User defined option to specify β explicitly.
shock-capturing stabilization
To display this section, click the Show button () and select Stabilization. Select Enable q-Laplacian relaxation to add some artificial nonlinear damping to the model (it is turned off per default). This is typically only necessary in highly nonlinear models. The dissipative term of physical origin will often balance the shock formation (remember to define the appropriate Fluid model in the Transient Pressure Acoustics Model). The effective diffusivity is tuned with the stabilization by adding an extra term that reads
The highest artificial damping is achieved where the acoustic pressure increases or decreases the most rapidly. It reaches its maximal values where the pressure endures discontinuities, that is, where shocks arise. Thus this technique provides a shock-capturing stabilization.
Specify the q-Laplacian exponent q and the q-Laplacian factor κ to get the desirable amount of artificial damping. Note that the damping must not be too high nor too low. The particular values of q and κ depend on the material and the input signal frequency. The two parameters that control the stabilization require manual tuning. A suggested approach is to use a simple 1D model to tune the parameters based on fluid material properties and frequency content. Use, for example, the Nonlinear Acoustics — Modeling of the 1D Westervelt Equation model from the application library to do so.
Nonlinear Acoustics — Modeling of the 1D Westervelt Equation: Application Library path Acoustics_Module/Nonlinear_Acoustics/nonlinear_acoustics_westervelt_1d
If the chosen fluid model has no dissipation (Linear elastic (the default) or Ideal Gas), a default sound dissipation δ = 2·10-5 m2/s will be used in the artificial damping term.