where u = u(r, t) is the particle velocity associated with the acoustic wave motion. The total  particle velocity is given by

where V denotes the local mean velocity for the fluid motion (the mean flow is labeled u0 in the linearized Euler and Navier-Stokes interfaces). The dynamic equations for this mean-flow field are described in the next subsection. For now, just assume V to be a given irrotational background velocity field; hence, also the mean-flow velocity can be defined in terms of a potential field Φ, by V = ∇Φ. 

The linearized equation for the velocity potential , governing acoustic waves in a background flow with mean background velocity V, mean background density ρ0, and mean background speed of sound c0, is

In deriving this equation, all variables appearing in the full nonlinear fluid-dynamics equations were first split in time-independent and acoustic parts, in the manner of Equation 4-9. Then, linearizing the resulting equations in the acoustic perturbation and eliminating all acoustic variables except the velocity potential gives Equation 4-10. Thus, the density ρ in this equation is the time-independent part. The corresponding acoustic part is ρ(r, t) = p(r, t)/c02 where p is the acoustic pressure, given by

Hence, once Equation 4-10 has been solved for the velocity potential, the acoustic pressure can easily be calculated.

When transformed to the frequency domain, the wave Equation 4-10 reads

In the frequency domain the velocity potential φ is assumed to be a harmonic wave of the form

the out-of-plane wave number kz enters the equations when the ∇ operators are expanded:

The default value of the out-of-plane wave number is 0, that is, no wave propagation perpendicular to the 2D plane. In a mode analysis the equations are solved for kz.

the azimuthal wave number m similarly  appears in the equation as a parameter:

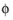
Here ρ0 (SI unit: kg/m3) is the background mean flow density, V (SI unit: m/s) denotes the background mean velocity, and c0 (SI unit: m/s) refers to the speed of sound. The software solves the equation for the velocity potential , with SI unit m2/s. The validity of this equation relies on the assumption that ρ0, V, and c0 are approximately constant in time, while they can be functions of the spatial coordinates.

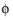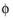
for the eigenmodes, , and eigenvalues, λ = −ikz, on a bounded two-dimensional domain, Ω, given well-posed edge conditions on ∂Ω. In this equation, is the velocity potential, ρ0 is the background mean flow density, c0 is the speed of sound, ω is the angular frequency, and kz is the out-of-plane wave number or propagation constant. Furthermore, Vt denotes the background mean velocity in the tangential plane while Vn is the background mean velocity component in the normal direction.