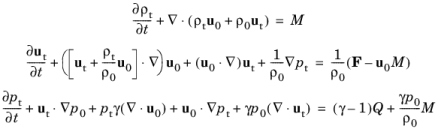The linearized Euler equations are derived from Euler’s equations, that is Equation 4-5 with no thermal conduction and no viscous losses. The fluid in the linearized Euler physics interface is assumed to be an ideal gas. The energy equation is also often written in terms of the pressure. This manipulation is possible using the thermodynamic differential for the entropy valid for an ideal gas. This is the common approach in literature. A review of the linearized Euler equations is found in, for example, Ref. 12 and Ref. 13.

Here, the subscript “1” has been dropped on the acoustic perturbation variables. The time derivatives are replaced with multiplication by iω in the frequency domain. And source terms include a mass source M, a volume force F, and a heat source Q.

It also follows from the governing equations and the thermodynamic relations that the acoustic variations in the specific entropy s and in the temperature T are given by

When the linearized Euler (LE) equations are solved in the time domain (or in the frequency domain with an iterative solver), linear physical instability waves can develop, the so-called Kelvin-Helmholtz instabilities. They are instabilities that grow exponentially because no losses exist in the LE equations (no viscous dissipation and no heat conduction). Furthermore, they are limited by non-linearities in the full Navier-Stokes flow equations. It has been shown that in certain cases the growth of these instabilities can be limited, while the acoustic solution is retained, by canceling terms involving gradients of the mean flow quantities. This is known as gradient terms suppression (GTS) stabilization. See more details in Ref. 9, Ref. 10, and Ref. 11.

Expressions for the energy flux, that is, the acoustic intensity vector, are often referred to as Myers’ energy corollary, see Ref. 15 and Ref. 16. The instantaneous intensity vector Ii is defined for both transient and frequency domain models as

The (time averaged) intensity vector I is given in the frequency domain by

The Linearized Euler, Frequency Domain Interface and The Linearized Euler, Transient Interface have an Impedance and Interior Impedance physics feature and its theory is included here.

In the frequency domain Myers’ equation (Ref. 1) gives an expression for the normal velocity at a boundary with a normal impedance condition. It is a so-called low-frequency approximation condition in the limit of very thin flow boundary layers (compared to the wavelength). Such conditions are used, for example, for porous lining conditions in ducts (Ref. 2). The condition is given by:

where the surface normal n here points out of the domain and is the surface normal impedance.

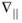
If the flow is parallel to the impedance boundary condition u0·n = 0, for example, slip flow over a mechanical impedance boundary condition (the same is true for the moving wall boundary condition described below), one can use a formulation with the tangential derivative () for the second term on the right-hand side:

where A is an arbitrary scalar.

The last term on the right-hand side of Equation 4-8 can be reformulated as follows:

Again these terms reduce significantly for the case where n⋅u0 = 0. If the boundary does not have curvature (planar boundary) then it is equal to zero. If the boundary is planar and the impedance condition is used inside the flow, for example at an outflow condition, then it reduces to the normal gradient of the velocity normal to the surface.

The Linearized Euler, Frequency Domain Interface and The Linearized Euler, Transient Interface have a Moving Wall physics feature and its theory is included here.

Myers’ equation (Ref. 1) gives the expressions used for a boundary condition at a moving wall. In the frequency domain it is given by

where un is the inward normal velocity is.

where the inward normal displacement is given by vn = −n⋅v (SI unit: m).