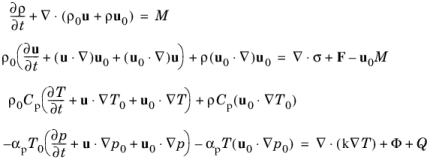The linearized Navier-Stokes equations are derived by linearizing the full set of fluid flow equations given in General Governing Equations. After some manipulation, the continuity, momentum, and energy equations and are:

where p, u, and T are the acoustic perturbations to the pressure, velocity, and temperature, respectively. In the frequency domain, the time derivatives of the dependent variables are replaced by multiplication with iω. The stress tensor is σ and Φ is the viscous dissipation function. The variables with a zero subscript are the background mean flow values and the subscript “1” is dropped on the acoustic variables.

The terms in the governing equations presented in Equation 4-6 can be divided into four categories. The time derivative (or frequency dependent) term, convective terms like u0 ⋅ ∇p, reactive terms like u ⋅ ∇p0, diffusive terms, and source terms. In many aeroacoustic formulations the reactive terms are removed (or simplified) from the governing equations in order to avoid the Kelvin-Helmholtz instabilities. This is sometimes referred to as gradient term stabilization (GTS).