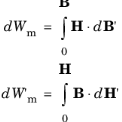The method of virtual work utilizes that, under constant magnetic flux conditions (
Ref. 5), the total magnetic force on a system is computed as
where 
is the rotational angle about the axis.
Under the condition of constant currents and linear materials, the total force and torque can be computed in the same way but with opposite signs,
Under the condition of constant currents and nonlinear materials, the total force and torque must be computed from the magnetic coenergy and with opposite signs,
Under the condition of constant charges, the total electric force and torque on a system are computed as
Under the condition of constant potentials and linear materials, the total electric force and torque on a system can be computed as
Under the condition of constant potentials and nonlinear materials, the total electric force and torque on a system must be computed from the electric coenergy as