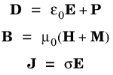To obtain a closed system, the equations include constitutive relations that describe the macroscopic properties of the medium. They are given as:
where ε0 is the permittivity of vacuum,
μ0 is the permeability of vacuum, and
σ is the electrical conductivity. In the SI system, the permeability of vacuum is chosen to be
4π·10−7 H/m. The velocity of an electromagnetic wave in a vacuum is given as
c0 and the permittivity of a vacuum is derived from the relation:
The electromagnetic constants ε0,
μ0, and
c0 are available in COMSOL Multiphysics as predefined physical constants.
The electric polarization vector P describes how the material is polarized when an electric field
E is present. It can be interpreted as the volume density of
electric dipole moments.
P is generally a function of
E. Some materials can have a nonzero
P also when there is no electric field present.
The magnetization vector M similarly describes how the material is magnetized when a magnetic field
H is present. It can be interpreted as the volume density of
magnetic dipole moments.
M is generally a function of
H. Permanent magnets, for instance, have a nonzero
M also when there is no magnetic field present.
For linear materials, the polarization is directly proportional to the electric field, P = ε0 χe E , where
χe is the electric susceptibility. Similarly in linear materials, the magnetization is directly proportional to the magnetic field,
M = χm H , where
χm is the magnetic susceptibility. For such materials, the constitutive relations are:
The parameter εr is the relative permittivity and
μr is the relative permeability of the material. Usually these are scalar properties but can, in the general case, be 3-by-3 tensors when the material is anisotropic. The properties
ε and
μ (without subscripts) are the permittivity and permeability of the material, respectively.
where Br is the
remanent magnetic flux density, which is the magnetic flux density when no magnetic field is present.