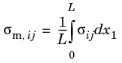Stress linearization is a procedure in which the stress distribution along a line through the thickness in a solid is approximated with an equivalent linear stress distribution, similar to what would be the result of an analysis using shell theory. The line is commonly referred to as a stress classification line, SCL.

First, the computed stresses are transformed into a local orthonormal coordinate system x1-x2-x3 where the x1 direction is oriented along the SCL. In 3D, you must specify the x2 direction, and thus implicitly the x3 direction. In 2D and 2D axial symmetry, the x3 direction is in the out-of-plane direction, that is the Z and azimuthal directions respectively.

The length of the SCL, which is assumed to be straight, start on one boundary, and end on the opposite boundary, is denoted L.

The membrane stress tensor is the average of each local stress component along the SCL:

Each component of the bending stress tensor is assumed to have a linear variation along the SCL, with the value being zero at the midpoint.

Finally the peak stress tensor is defined at the two end points of the SCL. It is the difference between the actual stress tensor, and the linearized stress representation.

The stress intensity, also known as the Tresca effective stress, is often the ultimate goal of a stress linearization. It is computed as a worst case of the effective stress at the two ends of the SCL. The stress intensity is computed from the principal stresses as