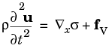Equation Implementation
The equilibrium equations for solid mechanics are given by Newton’s second law. It is usually written using a spatial formulation in terms of the Cauchy stress tensor σ:
Here fV is a body force per unit deformed volume, and ρ is the current mass density. For the material frame formulation used in COMSOL Multiphysics, it is more appropriate to use a Lagrangian version if the equation:
Now that the first Piola-Kirchhoff stress tensor, P, is used. FV is a body force with components in the current configuration but given with respect to the undeformed volume, and ρ0 is the initial mass density. Note the gradient operators are not the same: in the first case the gradient is taken with respect to the spatial coordinates, and in the second case with respect to the material coordinates. Using the more common second Piola-Kirchhoff stress tensor, S, the same equation reads
(3-51)
where F is the deformation gradient. The COMSOL Multiphysics implementation of the equations in the Solid Mechanics interface is however not based on the equation of motion directly, but rather on the principle of virtual work.
The principle of virtual work states that the sum of the internal virtual work and the external virtual work are equal. The internal virtual work is the work done by the current stress state on a kinematically admissible variation in strains. The external virtual work is the work done by all forces (acting on domains, boundaries, edges, or points) when multiplied with the variation in displacements corresponding to the variation in strains. The virtual displacements δu are in the finite element formulation represented by the test() operator in COMSOL Multiphysics. For a stationary case, the virtual work δW is written as
The strains are computed from the gradients of the displacements, and the stresses are given by the constitutive relation.
In a dynamic analysis, the inertial forces are included in the volume forces, according to d’Alembert’s principle.
(3-52)
Since the equations are formulated on the material frame, all integrals are taken over the undeformed geometry. The stress and strain contributions must be interpreted differently depending on whether the formulation is geometrically nonlinear or not.
•
If the study step is geometrically linear, the strain ε is the engineering strain. The stress σ could in principle be any of the stress measures, as they all converge to the same engineering stress in this case.
•
If the study step is geometrically nonlinear, the strain ε is the Green-Lagrange strain and the stress σ is the second Piola-Kirchhoff stress.
The Solid Mechanics interface supports Stationary (static), Eigenfrequency, Time Dependent (transient), Frequency Domain, and Modal solver study types as well as linear buckling.
Frequency-Domain Studies
In the frequency domain, the frequency response is studied when applying harmonic loads. Harmonic loads are specified using two components:
•
The amplitude value in direction m, Fm
•
The corresponding phase,
To derive the equations for the linear response from harmonic excitation loads
Assume a harmonic response with the same angular frequency as the excitation load
The relationship can also be described using complex notation with
and
The primary results, such as displacements, velocities, accelerations, and stress and strain components are all complex valued.
Eigenfrequency Studies
The eigenfrequency equations are derived by assuming a harmonic displacement field, similar as for the frequency response formulation. The difference is that this study type uses a new variable jω explicitly expressed in the eigenvalue jω = −λ. The eigenfrequency f is then derived from jω as
Damped eigenfrequencies can also be studied, so λ is not necessarily a purely imaginary number. Any damping included in the problem will automatically cause the eigenfrequencies to become complex valued.
In addition to the eigenfrequency, the quality factor, Q, and decay factor, δ, for the model can be examined:
Linear Buckling
The linear buckling analysis consists of two steps. First a stationary problem is solved using a unit load of arbitrary size. The critical load is then obtained by solving an eigenvalue problem, where the eigenvalue λ is the multiplier to the original load that would cause buckling.
For a general introduction, see Linearized Buckling Analysis
The formulation in terms of virtual work is
(3-53)
Here ε us the engineering strain, εGL is the Green-Lagrange strain and σ1 is the stress caused by the unit load. In terms of stiffness matrices, this corresponds to
where KL is the linear stiffness matrix, and KNL is the nonlinear contribution to the full stiffness matrix. The symbolic linearization point u0 is the displacement vector caused by the unit load.
Strictly speaking, this formulation assumes that geometric nonlinearity is not used in the eigenvalue step. The Green-Lagrange tensor is inserted explicitly in the second term of Equation 3-53, while the first term uses the linear (engineering) strain tensor.
If, however, geometric nonlinearity is selected, then Equation 3-53 is replaced by
By using the term (λ-1), the effect of using the Green-Lagrange strain tensor in the first term is to a large extent removed. Unless the unit load is significantly larger than the buckling load, the result will be the same as the intended, even if geometric nonlinearity was inadvertently selected in the eigenvalue study step.