The Cam-clay material model was developed at the University of Cambridge in the 1970s, and since then it has experienced different modifications. The modified Cam-clay model is the most commonly used due to the smooth yield surface, and it is the one implemented in the Geomechanics Module.

The Cam-clay model is a so-called critical state model, where the loading and unloading of the material follows different trajectories in stress space. The model also features hardening and softening of clays. Different formulations can be found in textbooks about these models (see Ref. 13, Ref. 14, and Ref. 15).

This is an ellipse in p-q plane, with a cross section independent of Lode angle and smooth for differentiation. Note that p, q, and pc are always positive variables.

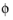
The material parameter M > 0 defines the slope of a line in the p-q space called critical state line, and it can be related to the angle of internal friction in the Mohr-Coulomb criterion

In the Cam-clay model, hardening is controlled by the consolidation pressure pc, which depends exponentially on the volumetric plastic strain εpl,vol.

Here, the parameter pc0 is the initial consolidation pressure, and the exponent Bpl is a parameter which depends on the initial void ratio e0, the swelling index κ, and the compression index λ:

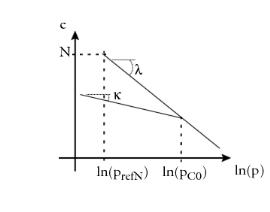
In this formulation, the compression index λ is the slope of the virgin isotropic consolidation line, and κ is the slope of the rebound-reloading line (also called loading-reloading line) in the e versus ln(p) plane.

Here, σ is the Cauchy stress tensor, ε is the total strain tensor, εinel is the inelastic strain tensor, σ0 is the initial stress tensor, and C is the fourth-order elasticity tensor.

here p0 = − trace(σ0)/3 is the trace of the initial stress tensor σ0, and K is the bulk modulus, a constant parameter independent of the stress or strain.

and K0 a reference bulk modulus. This formulation gives a tangent bulk modulus KT = −Bel(p−p0). The reference bulk modulus is calculated from the initial consolidation pressure pc0, and the void ratio at reference pressure N.

The associated flow rule (Qp = Fy) and the yield surface written in terms of these two invariants, Fy(I1, J2), gives a rate equation for the plastic strain tensor calculated from the derivatives of Fy with respect to the stress tensor σ

The trace of the plastic strain rate tensor (the volumetric plastic strain rate ) then reads

This relation explains the reason why there is isotropic hardening for p > pc/2 and isotropic softening for p < pc/2. So the volumetric plastic strain can either increase or decrease.

In the Cam-clay model, the hardening is controlled by the consolidation pressure variable as a function of volumetric plastic strain, as written in Equation 3-35. Hardening introduces changes in the shape of the Cam-clay ellipse, since its major semi-axis depends on the value of pc.

When a pore fluid pressure pf is added to the Cam-clay material, the yield surface is shifted on the p axis

The quantity p − pf is normally regarded as the effective pressure, or effective stress, which should not be confused with von Mises stress.