A hyperelastic material is defined by its elastic strain energy density Ws, which is a function of the elastic strain state. It is often referred to as the energy density. The hyperelastic formulation normally gives a nonlinear relation between stress and strain, as opposed to Hooke’s law in linear elasticity.

Most of the time, the right Cauchy-Green deformation tensor C is used to describe the current state of strain (although one could use the left Cauchy-Green tensor B, the deformation gradient tensor F, and so forth), so the strain energy density is written as Ws(C).

For isotropic hyperelastic materials, any state of strain can be described in terms of three independent variables—common choices are the invariants of the right Cauchy-Green tensor C, the invariants of the Green-Lagrange strain tensor, or the principal stretches.

In the general case, the expression for the energy Ws is symbolically evaluated down to the components of C using the invariants definitions prior to the calculations of the components of the second Piola-Kirchhoff stress tensor. The differentiation is performed in components on the local coordinate system.

If thermal expansion is present, a stress-free volume change occurs. This is a pure volumetric change, so the multiplicative decomposition of the deformation gradient tensor in Equation 3-4 implies

Here, the thermal volume ratio, Jth, depends on the thermal stretch λth, which for linear thermal expansion in isotropic materials can be written in terms of the isotropic coefficient of thermal expansion, αiso, and the absolute change in temperature

Here, the term αiso(T−Tref) is the thermal strain. The isotropic thermal gradient is therefore a diagonal tensor defined as

When the coefficient of thermal expansion α is anisotropic, the thermal strain is computed from

where βh is the coefficient of hygroscopic swelling, cmo is the moisture concentration, and cmo,ref is the strain-free reference concentration. The coefficient of hygroscopic swelling can represent isotropic or anisotropic swelling. The anisotropic hygroscopic gradient is defined as

Here, the plastic deformation tensor Fpl depends on the plastic flow rule, yield function, and plastic potential.

For some classes of hyperelastic materials it is convenient to split the strain energy density into volumetric (also called dilatational) and isochoric (also called distortional or volume-preserving) contributions. The elastic deformation tensor is then multiplicatively decomposed into the volumetric and isochoric components

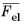
with Fel,vol as the volumetric elastic deformation (a diagonal tensor) and the isochoric elastic deformation gradient. Isochoric deformation means that the volume ratio is kept constant during deformation, so the isochoric elastic deformation is computed by scaling it by the elastic volume ratio. The elastic volume ratio is defined by

By using Jel it is possible to define the isochoric-elastic deformation gradient

the isochoric-elastic right Cauchy-Green tensor

and the isochoric-elastic Green-Lagrange strain tensor

Some authors call 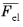and 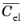the modified tensors. Note that

The other two invariants normally used together with Jel are the first and second invariant of the isochoric-elastic right Cauchy-Green deformation tensor

If the Nearly incompressible material check box is selected for the Hyperelastic Material node, the total elastic energy function is split into two parts as:

where Wiso is the isochoric strain energy density and Wvol is the volumetric strain energy density.

The volumetric strain energy density, Wvol, can only be defined as an expression of the elastic volumetric deformation. The most commonly used form is:

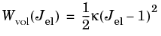
where κ is the initial bulk modulus. From here, the volumetric stress (pressure) is calculated as

When the expression in Equation 3-19 is used, the pressure becomes linearly related to the volume change:

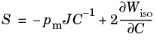
A numerical scheme is said to exhibit locking if the accuracy of the approximation deteriorates as a parameter tends to a limiting value (Ref. 11). Finite elements in solid mechanics are said to “lock” when exhibiting an unphysical response to deformation (Ref. 12). Locking can occur for many different reasons. For linear elastic materials, this typically happens as Poisson’s ratio tends to 0.5, or the bulk modulus is much larger than the shear modulus. Numerical errors arise because the shape functions are unable to properly describe the volume preserving deformation.

To avoid the locking problem in computations, the mixed formulation replaces pm in Equation 3-20 with a corresponding interpolated pressure help variable pw, which adds extra degrees of freedom to the ones defined by the displacement vector u.

The general procedure is the same as when the Nearly incompressible material check box is selected for the Linear Elastic Materials node.

The strain energy density for the compressible version of the Neo-Hookean material is written in terms of the elastic volume ratio Jel and the first invariant of the elastic right Cauchy-Green deformation tensor I1(Cel) (Ref. 10).

Here, λ and μ are the Lamé coefficients.

The elastic strain energy density is written with two parameters (the two Lamé coefficients) and two invariants of the elastic Green-Lagrange strain tensor, I1(εel) and I2(εel)

Here, λ and μ are the Lamé parameters.

The nearly incompressible version uses the isochoric invariants and , and the initial bulk modulus κ is calculated from the Lamé parameters κ = λ+2μ/3

The material parameters C10 and C01 are related to the Lamé parameter μ = 2(C10+C01).

Rivlin and Saunders (Ref. 2) proposed a phenomenological model for small deformations in rubber-based materials on a polynomial expansion of the first two invariants of the elastic right Cauchy-Green deformation, so the strain energy density is written as an infinite series

with C00 = 0. This material model is sometimes also called polynomial hyperelastic material.

Here, κ is the initial bulk modulus.

Yeoh proposed (Ref. 1) a phenomenological model in order to fit experimental data of filled rubbers, where Mooney-Rivlin and Neo-Hookean models were to simple to describe the stiffening effect in the large strain regime. The strain energy was fitted to experimental data by means of three parameters, and the first invariant of the elastic right Cauchy-Green deformation tensors I1(Cel)

The Neo-Hookean material model usually fits well to experimental data at moderate strains but fails to model hyperelastic deformations at high strains. In order to model rubber-like materials at high strains, Ogden adapted (Ref. 1) the energy of a Neo-Hookean material to

Here αp and μp are material parameters, and λel1, λel2, and λel3 are the principal elastic stretches such as Jel = λel1λel2λel3.

The Ogden model is empirical, in the sense that it does not relate the material parameters αp and μp to physical phenomena. The parameters αp and μp are obtained by curve-fitting measured data, which can be difficult for N > 2. The most common implementation of Ogden material is with N = 2, so four parameters are needed.

The Storakers material (Ref. 12 and Ref. 15) is used to model highly compressible foams. The strain energy density is written in a similar fashion as in Ogden material:

The initial shear and bulk moduli can be computed from the parameters μk and βk as

for constant parameters βk = β, the initial bulk modulus becomes κ = 2μ(β + 1/3), so a stable material requires μ > 0 and β > −1/3. In this case, the Poisson's ratio is given by ν = β/(2β+2/3), which means that for a Poisson’s ratio larger than −1, β > −2/9 is needed.

The Varga material model (Ref. 1) describes the strain energy in terms of the elastic stretches as

The simplest Varga model is obtained by setting c1 = μ and c2 = 0:

Arruda and Boyce (Ref. 3) derived a material model based on Langevin statistics of polymer chains. The strain energy density is defined by

Here, μ0 is the initial macroscopic shear modulus, I1(Cel) is the first invariant of the elastic right Cauchy-Green deformation tensor, and the coefficients cp are obtained by series expansion of the inverse Langevin function.

Arruda and Boyce truncated the series and used only the first five terms as listed in Table 3-2:

Other authors (Ref. 1) use only the first three coefficients of the series. The number of segments in the polymeric chain is specified by the parameter N so the material model is described by only two parameters, μ0 and N.

This material model is sometimes also called the eight-chain model since it was derived for N = 8.

Many hyperelastic material models are difficult to fit to experimental data. Gent material (Ref. 13 and Ref. 14) is a simple phenomenological constitutive model based on only two parameters, μ and jm, which defines the strain energy density as:

Here, μ is the shear modulus and jm is a limiting value for I1− 3, which takes care of the limiting polymeric chain extensibility of the material.

Since the strain energy density does not depend on the second invariant I2, the Gent model is often classified as a generalized Neo-Hookean material. The strain energy density tends to be the one of incompressible Neo-Hookean material as .

The Blatz-Ko material model was developed for foamed elastomers and polyurethane rubbers, and it is valid for compressible isotropic hyperelastic materials (Ref. 1).

The elastic strain energy density is written with three parameters and the three invariants of the elastic right Cauchy-Green deformation tensor, I1(Cel), I2(Cel), and I3(Cel)

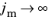
Here, φ is an interpolation parameter bounded to 0 < φ < 1, µ is the shear modulus, and β is an expression of Poisson’s ratio.

In the special case of φ = 1, the strain energy reduces to a similar form of the Neo-Hookean model

Gao proposed (Ref. 16) a simple hyperelastic material where the strain energy density is defined by two parameters, a and n, and two invariants of the elastic right Cauchy-Green deformation tensors Cel:

Here, the invariant I-1(Cel) is calculated as:

Gao proposed that the material is unconditionally stable when the parameters are bounded to 3 > n > 1 and a > 0, and related these parameters under small strain to the Young’s modulus and Poisson’s ratio by:

Since n = (1+ν)/(1−2ν) and it is bounded to 1 < n < 3, this material model is stable for materials with an initial Poisson’s ratio in the range of 0 < ν < 2/7.

The Murnaghan potential is used in nonlinear acoustoelasticity. Most conveniently it is expressed in terms of the three invariants of the elastic Green-Lagrange strain tensor, I1(εel), I2(εel), and I3(εel)

Here, l, m, and n are the Murnaghan third-order elastic moduli, which can be found experimentally for many commonly encountered materials such as steel and aluminum, and λ and μ are the Lamé parameters.

When a material model is user-defined, an expression for the elastic strain energy Ws is entered, which can include any expressions involving the following: