In the frequency domain, these can be represented by introducing complex material properties in the elasticity and permittivity matrices, respectively. Taking the mechanical case as an example, this introduces a phase lag between the stress and the strain, which corresponds to a Hysteretic Loss. These losses can be added to the Piezoelectric Material by three subnodes: Mechanical Damping, Coupling Loss, and Dielectric Loss. The losses typically defined as loss factors (see below).

Low frequency losses, corresponding to a finite material conductivity, can be added to the model through an Electrical Conductivity (Time Harmonic) subnode. This feature operates only in the frequency domain.

In the time domain, the losses can be added by using the Rayleigh Damping option in the Mechanical Damping and Coupling Loss subnodes, and by using the Dielectric Dispersion option in the Dielectric Loss subnodes. These types of damping are also available in the frequency domain.

In the frequency domain, the dissipative behavior of the material can be modeled using complex-valued material properties, irrespective of the loss mechanism. Such hysteretic losses can be applied to model both electrical and mechanical losses. For the case of piezoelectric materials, this means that the constitutive equations are written as follows.

where 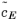, , 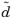and ε are complex-valued matrices, where the imaginary part defines the dissipative function of the material.

where the sign depends on the material property used. The loss factors are specific to the material property, and thus they are named according to the property they refer to, for example, ηcE. For a structural material without coupling, simply use ηs, the structural loss factor.

where m and n refer to components of each matrix.

For more information about hysteretic losses, see Ref. 1 to Ref. 4.

For frequency domain analyses, the electrical conductivity of the piezoelectric material (see Ref. 2, Ref. 5, and Ref. 6) can be defined. Depending on the formulation of the electrical equation, the electrical conductivity appears in the equation as an effective electric displacement

where σe is the material electrical conductivity, and E is the electric field. Note that the displacement current variables themselves do not contain any conductivity effects.

Both a dielectric loss factor and the electrical conductivity can be defined at the same time. In such case, ensure that the loss factor refers to the alternating current loss tangent, which dominates at high frequencies, where the effect of ohmic conductivity vanishes (Ref. 7).

where two material parameters can be specified, the relaxation time τd, and the relative permittivity increment ΔεrS. The latter can be either a matrix or a scalar quantity. This model is a one-term version of the more general Debye dispersion model, Ref. 13. In the frequency domain, the time derivative is replaced by the factor jω, and the above equation can be rewritten as

which shows how the dispersion parameters contribute into the polarization and losses. Thus, the effective permittivity varies from εrS + ΔεrS down to ε0εrS as the excitation frequency increases from zero. The damping effect vanishes for both large and small frequencies, and it reaches the maximum for ω = 1/τd.