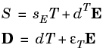Piezoelectric materials become electrically polarized when strained. From a microscopic perspective, the displacement of atoms within the unit cell (when the solid is deformed) results into electric dipoles within the medium. In certain crystal structures, this combines to give an average macroscopic dipole moment or electric polarization. This effect, known as the direct piezoelectric effect, is always accompanied by the converse piezoelectric effect, in which the solid becomes strained when placed in an electric field.

Here, the naming convention used in piezoelectricity theory is assumed: S is the strain, T is the stress, E is the electric field, and D is the electric displacement field. The material parameters sE, d, and εT, correspond to the material compliance, the coupling properties and the permittivity. These quantities are tensors of rank 4, 3, and 2 respectively. The tensors however are highly symmetric for physical reasons, and they can be represented as matrices within an abbreviated subscript notation, which is usually more convenient. In the Piezoelectric Devices interface, the Voigt notation is used, which is standard in the literature for piezoelectricity but which differs from the defaults in the Solid Mechanics interface.

Equation 2-13 will, using the notation from structural mechanics, then read

Equation 2-13 (or Equation 2-14) is known as the strain-charge form of the constitutive relations. The equation can be re-arranged into the stress-charge form, which relates the material stresses to the electric field:

The material properties, cE, e, and εS are related to sE, d, and εT. It is possible to use either form of the constitutive relations. In addition to Equation 2-13 or Equation 2-15, the equations of solid mechanics and electrostatics must also be solved within the material.