The relations μH = ∇ × A and
E = −∂A/∂t make it possible to rewrite Maxwell-Ampère’s law using the magnetic potential.
This is the equation used by The Electromagnetic Waves, Transient Interface. It is suitable for the simulation of non-sinusoidal waveforms or non linear media.
Using the relation εr =
n2, where
n is the refractive index, the equations can alternatively be written
The TM waves polarization has only one magnetic field component in the z direction, and thus the electric field and vector potential lie in the modeling plane. Hence it is obtained by solving only for the in-plane vector potential components. The equation is formally the same as in 3D, the only difference being that the out-of-plane vector potential component is zero everywhere and that out-of-plane spatial derivatives are set to zero.
As the field propagates in the modeling xy-plane a TE wave has only one non zero vector potential component, namely in the
z direction. The magnetic field lies in the modeling plane. Thus the equation in the time domain can be simplified to a scalar equation for
Az:
Using the relation εr =
n2, where
n is the refractive index, the equation can alternatively be written
When using the refractive index, the assumption is that μr = 1 and
σ = 0 and only the constitutive relations for linear materials can be used.
TM waves have a magnetic field with only a 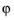 component and thus an electric field and a magnetic vector potential with components in the rz
component and thus an electric field and a magnetic vector potential with components in the rz-plane only. The equation is formally the same as in 3D, the only difference being that the
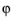
component is zero everywhere and that spatial derivatives with respect to
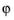
are set to zero.