
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click Study.
|
|
5
|
|
6
|
Click Done.
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
Select the object c2 only.
|
|
3
|
|
4
|
|
5
|
Select the object c1 only.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
Select the object c4 only.
|
|
3
|
|
4
|
|
5
|
Select the object c3 only.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
Click in the Graphics window and then press Ctrl+A to select all objects.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Free Molecular Flow (fmf) click Molecular Flow 1.
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Free Molecular Flow (fmf) click Surface Temperature 1.
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
1
|
|
1
|
|
2
|
Click in the Graphics window and then press Ctrl+A to select all domains.
|
|
3
|
|
4
|
|
5
|
Clear the Pressure check box.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Model>Component 1>Free Molecular Flow>Number density>fmf.n_G - Number density.
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for Global Evaluation, click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Model>Component 1>Definitions>Variables>alpha - Transmission probability.
|
|
3
|
Click Evaluate.
|
|
1
|
|
2
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for Study 1.
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve check box for the Free Molecular Flow (fmf) interface.
|
|
5
|
|
6
|
|
1
|
|
2
|
In the Settings window for Mathematical Particle Tracing, locate the Particle Release and Propagation section.
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Mathematical Particle Tracing (pt) and choose Outlet.
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Mathematical Particle Tracing (pt) click Wall 1.
|
|
2
|
|
3
|
|
4
|
Locate the General Reflection Settings section. Select the Specify tangential and normal velocity components check box.
|
|
5
|
|
1
|
In the Model Builder window, right-click Mathematical Particle Tracing (pt) and choose the boundary condition Particle Counter.
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Mathematical Particle Tracing (pt) click Particle Properties 1.
|
|
2
|
|
3
|
|
1
|
|
2
|
Click in the Graphics window and then press Ctrl+A to select all domains.
|
|
3
|
|
4
|
|
5
|
|
6
|
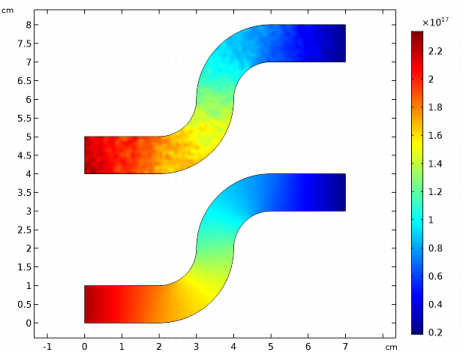
Locate the Units section. Find the Dependent variable quantity subsection. From the list, choose Number density (1/m^3).
|
|
7
|
|
1
|
|
2
|
|
3
|
Click Range.
|
|
4
|
|
5
|
|
6
|
|
7
|
Click Replace.
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click Replace Expression in the upper-right corner of the Expressions section. From the menu, choose Model>Component 1>Mathematical Particle Tracing>Particle Counter 1>pt.pcnt1.alpha - Transmission probability.
|
|
6
|
Click Evaluate.
|
|
1
|
Go to the Table window.
|
|
1
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
Click to expand the Inherit style section. Locate the Inherit Style section. From the Plot list, choose Surface 1.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Results>Number Density Comparison right-click Line 1 and choose Paste Deformation.
|
|
2
|
|
3
|
|
4
|