
|
|
1
|
|
2
|
Compute the electric potential due to the space charge density of the beam, using a stationary solver. The model uses an Infinite Element Domain region to apply appropriate boundary conditions for a beam propagating in free space.
|
|
1
|
|
2
|
In the Select Physics tree, select AC/DC>Particle Tracing>Particle Field Interaction, Non-Relativistic.
|
|
3
|
Click Add.
|
|
4
|
Click Study.
|
|
5
|
In the Select Study tree, select Preset Studies for Selected Physics Interfaces>Bidirectionally Coupled Particle Tracing.
|
|
6
|
Click Done.
|
|
1
|
|
2
|
|
3
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file electron_beam_divergence_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click to expand the Layers section. In the table, enter the following settings:
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
On the object cyl1, select Boundary 10 only.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Charged Particle Tracing (cpt) and choose Inlet.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Charged Particle Tracing (cpt) click Electric Force 1.
|
|
3
|
|
4
|
|
5
|
Locate the Advanced Settings section. Select the Use piecewise polynomial recovery on field check box.
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Electrostatics (es) and choose Ground.
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose Free Tetrahedral.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Settings window for Bidirectionally Coupled Particle Tracing, locate the Study Settings section.
|
|
2
|
Click Range.
|
|
3
|
|
4
|
|
5
|
Click Replace.
|
|
6
|
|
7
|
|
8
|
|
9
|
|
10
|
|
11
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
5
|
Click Range.
|
|
6
|
|
7
|
|
8
|
|
9
|
Click Replace.
|
|
10
|
|
1
|
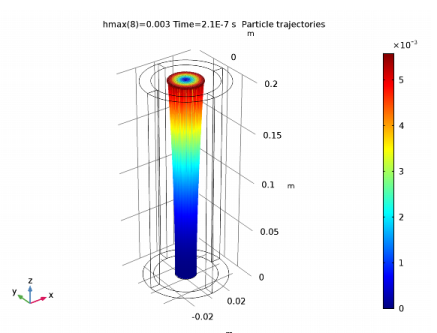
In the Model Builder window, expand the Results>Particle Trajectories (cpt) node, then click Particle Trajectories 1.
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, expand the Particle Trajectories 1 node, then click Color Expression 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
In the Settings window for Global, type Relative Error in Longitudinal Beam Displacement in the Label text field.
|
|
3
|
|
4
|