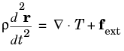where ρ is the density, r denotes the position of a point fixed in the material at time t=0, T is the stress tensor, and fext is an external volume force, such as gravity (fext = ρg). If a linear elastic material is added to the Electromechanics interface, this equation is solved in the absence of an electric field.

where T1 and T2 represent the stress tensor in Materials 1 and 2, respectively, and n1 is the normal vector pointing out from the domain containing Material 1.