Thin-Film Flow
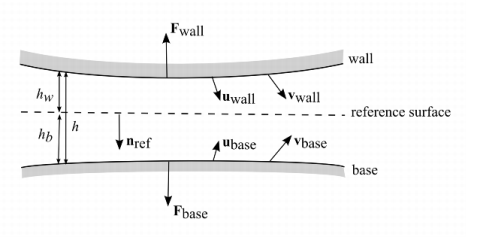
Figure 4-2 shows a typical configuration for the flow of fluid in a thin layer. The upper boundary is referred to as the wall, and the lower boundary is referred to as the base. Damping or lubrication forces operate on both surfaces.
In many cases the gap is sufficiently small for the flow in the thin film to be isothermal. Usually the gap thickness, h, is much smaller than the lateral dimensions of the geometry, L. If this is the case it is possible to neglect inertial effects in the fluid in comparison to viscous effects (for MEMS devices this assumption is reasonable below MHz frequencies). Additionally, the curvature of the reference surface can be ignored when h/L«1. Under these assumptions the Reynolds equation applies. For gas flows under the same conditions it is possible to derive a modified form of the Reynolds Equation, which uses the ideal gas law to eliminate the density from the equation system. Such a modified Reynolds equation can even be adapted to model the flow of rarefied gases.
Different terminology is used for thin-film flow in different fields of physics. In tribology the term lubrication is frequently used, especially when the fluid is a liquid. In resonant MEMS devices, flow in the thin layer of gas separating a device from the substrate on which it is fabricated often provides significant damping. In this case there is usually a distinction between squeezed-film damping, when the direction of motion of the structure is predominantly perpendicular to the reference plane, and slide-film damping for motion predominantly parallel to the reference plane.
Figure 4-2: An example illustrating a typical configuration for thin-film flow. A reference surface with normal nref sits in a narrow gap between a wall and base. In COMSOL the vector nref points into the base and out of the wall. The wall moves with a displacement uwall and velocity vwall from its initial position. Similarly the base moves from its initial position with displacement ubase and velocity vbase. The compression of the fluid results in an excess pressure, pf, above the reference pressure, pref, and a fluid velocity in the gap. At a point on the reference surface the average value of the fluid velocity along a line perpendicular to the surface is given by the in plane vector vave. The motion of the fluid results in forces on the wall (Fwall) and on the base (Fbase). The distance to the wall above the reference surface is hw while the base resides a distance hb below the reference surface. The total size of the gap is h=hw+hb. At a given time hw=hw1−nref ⋅uwall and hb=hb1−nref ⋅uwall where hw1 and hb1 are the initial distances to the wall and base, respectively.