The following correlations correspond to equations 9.26 and 9.27 in Ref. 18:

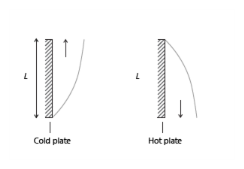
where the height of the wall, L, is a correlation input and

where in turn g is the acceleration of gravity equal to 9.81 m/s2. All material properties are evaluated at (T + Text) ⁄ 2. This correlation is valid for 104≤ RaL ≤ 1013.

The following correlations correspond to equations 9.26 and 9.27 in Ref. 18 (the same as for a vertical wall):

where the length of the wall, L, is a correlation input and ϕ is the tilt angle (the angle between the wall and the vertical direction; ϕ = 0 for vertical walls). These correlations are valid for −60° < ϕ < 60° and 104≤ RaL ≤ 1013.

The definition of the Raleigh number, RaL, is analogous to the one for vertical walls and is given by the following:

where in turn g denotes the gravitational acceleration, equal to 9.81 m/s2.

For turbulent flow, 1 is used instead of cos φ in the expression for h, because this gives better accuracy (see Ref. 38).

The laminar-turbulent transition depends on φ (see Ref. 38). Unfortunately, little data is available about transition. There is some data available in Ref. 38 but this data is only approximative, according to the authors. In addition, data is only provided for water (Pr around 6). For this reason, the flow is defined as turbulent, independently of the φ value, when

All material properties are evaluated at (T + Text) ⁄ 2.

The following correlations correspond to equations 9.30–9.32 in Ref. 18 but can also be found as equations 7.77 and 7.78 in Ref. 38.

If T > Text, then

while if T ≤ Text, then

RaL is given by Equation 4-126, and L, the characteristic length (defined as area/perimeter, see Ref. 38) is a correlation input. The material data are evaluated at (T + Text) ⁄ 2.

Equation 4-129 is used when T ≤ Text and Equation 4-130 is used when T > Text. Otherwise it is the same implementation as for Horizontal Plate, Upside.

The following correlations correspond to equations 9.34 in Ref. 18. It is validated for RaD ≤ 1012.

Here D is the cylinder diameter and RaD is given by

The following correlations correspond to equation 9.35 in Ref. 18. It is validated for RaD ≤ 1011 and Pr ≥ 0.7.

Here D is the cylinder diameter and RaD is given by

The following correlation corresponds to equation 7.83 in Ref. 38. It is validated only for side walls of the thin cylinder (δT ≥ D), the horizontal disks (top and bottom) should be treated as horizontal plates. If the boundary thin layer is much smaller than D, vertical wall correlations should be used.

where D is the cylinder diameter, H is the cylinder height, and RaH is given by