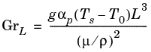In cases of externally driven flow, such as forced convection, the nature of the flow is characterized by the Reynolds number, Re, which describes the ratio of the inertial forces to the viscous forces. However, the velocity scale is initially unknown for internally driven flows such as natural convection. In such cases the Grashof number, Gr, characterizes the flow. It describes the ratio of the time scales for viscous diffusion in the fluid and the internal driving force (the buoyancy force). Like the Reynolds number it requires the definition of a length scale, the fluid’s physical properties, and the temperature scale (temperature difference). The Grashof number is defined as:

where  g is the acceleration of gravity, αp is the fluid’s coefficient of thermal expansion, Ts denotes the temperature of the hot surface, T0 equals the temperature of the surrounding air, L is the length scale, μ represents the fluid’s dynamic viscosity, and ρ its density.

In general, the coefficient of thermal expansion αp is given by

The transition from laminar to turbulent flow occurs at a Gr value of 109; the flow is turbulent for larger values.

The Rayleigh number, Ra, is another indicator of the regime. It is similar to the Grashof number except that it accounts for the thermal diffusivity: Ra = Pr Gr. A small value of the Ra number indicates that the conduction dominates. It such case using heat transfer coefficients to model convective heat transfer is not relevant. Instead, modeling the fluid as immobile is likely to be accurate.