Wavelength Dependence of Surface Emissivity and Absorptivity
The surface properties for radiation, the emissivity, and absorptivity can be dependent on the angle of emission or absorption, the surface temperature, or the radiation wavelength. The emissivity and absorptivity are defined in Ref. 17.
The Surface-to-Surface Radiation interface in the Heat Transfer module implements the radiosity method that enables arbitrary temperature dependence and assumes that the emissivity and absorptivity is independent of the angle of emission and absorption. It is also possible to account for wavelength dependence on the surface emissivity and absorptivity.
Planck Spectral Distribution
The Planck’s distribution of emissive power for a blackbody in vacuum is given as a function of surface temperature and wavelength.
The blackbody hemispherical emissive power (SI unit: W/(m3·sr)), is denoted eb, λ(λ, T), and defined as (1-37 in Ref. 17):
(4-72)
where:
•
the two constants C1 (SI unit: W·m2/sr) and C2 (SI unit: m·K) are given by
•
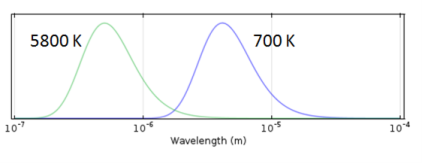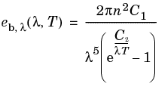
h is the Planck constant (SI unit: J·s)
•
kB is the Boltzmann constant (SI unit: J/K)
•
c0 is the speed of the light in vacuum (SI unit: m/s)
•
λ is the wavelength in vacuum (SI unit: m)
•
n is the refractive index of the media (SI unit: 1), equal to 1 in vacuum
Figure 4-6 and Figure 4-7 show the hemispherical spectral emissive power for a blackbody at 5780 K (the Sun’s blackbody temperature) and for a blackbody at 300 K. The dotted vertical lines delimit the visible spectrum (from 0.4 µm to 0.7 µm).
Figure 4-6: Planck distribution of a blackbody at 5780 K.
Figure 4-7: Planck distribution of a blackbody at 300 K.
The integral of eb, λ(λ, T) over a spectral band represents the power radiated on the spectral band and is defined by
where is the fractional blackbody emissive power,
Recall the Stefan-Boltzmann law that computes the power radiated across all wavelengths:
where n is the refractive index, and σ is the Stefan-Boltzmann constant equal to 5.67 ⋅ 10-8 W/(m2·K4). The power radiated in the spectral band [λ1, λ2] becomes:
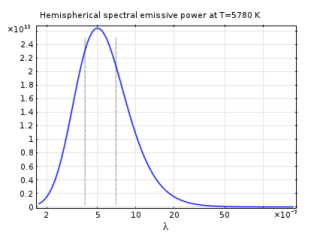
The function eb(T) is available as a predefined function via ht.feb(T) in the Heat Transfer interfaces.
Notice that:
and
The figure below shows the value of for different values of λT.
Diffuse-Gray Surfaces
Diffuse-gray surfaces correspond to the hypothesis that surface properties are independent of the radiation wavelength and angle between the surface normal and the radiation direction.
The assumption that the surface emissivity is independent of the radiation wavelength is often valid when most of the radiative power is concentrated on a relatively narrow spectral band. This is likely the case when the radiation is emitted by a surface at temperatures in limited range.
This setting is rarely applicable if there is solar radiation.
Solar and Ambient Spectral Bands
When solar radiation is part of the model, it is possible to enhance a diffuse-gray surface model by considering two spectral bands: one for short wavelengths and one for large wavelengths.
It is interesting to notice that about 97% of the radiated power from a blackbody at 5800 K is at wavelengths of 2.5 µm or shorter, and 97% of the radiated power from a blackbody at 700 K is at wavelengths of 2.5 µm or longer (see Figure 4-8).
Figure 4-8: Normalized Planck distribution of blackbodies at 700 K and 5800 K.
Many problems have a solar load, but the peak temperatures are below 700 K.
In such cases, it is appropriate to use a two-band approach with
•
A solar band for wavelengths shorter than 2.5 µm
•
An ambient band for wavelengths above 2.5 µm
For each surface, properties are then described in terms of a solar absorptivity and an emissivity.
Figure 4-9: Absorption of solar radiation and emission to the surroundings.
By splitting the bands at the default of 2.5 μm, the fraction of absorbed solar radiation on each surface is defined primarily by the solar absorptivity.
The reradiation at longer wavelengths (objects below ~700 K) and the reabsorption of this radiation is defined primarily via the emissivity
Figure 4-10: Solar and ambient spectral band approximation of the surface emissivity by a constant per band emissivity.
General diffuse-spectral surfaces
Diffuse-spectral surfaces correspond to the hypothesis that surface properties are wavelength dependent but independent of the angle between the surface normal and the radiation direction.
The heat transfer module enables to define constant surface properties per spectral bands (with up to 5 spectral bands) and to adjust spectral intervals endpoints.
The multiple spectral bands approach is used in cases when the surface emissivity varies significantly over the bands of interest.