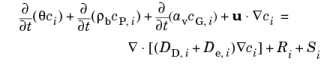The following equations for the concentrations, ci, describe the transport of solutes in a variably saturated porous medium for the most general case, when the pore space is primarily filled with liquid but also contain pockets or immobile gas:
On the left-hand side of Equation 5-11, the first three terms correspond to the accumulation of species within the liquid, solid, and gas phases, while the last term describes the convection due to the velocity field
u (SI unit: m/s).
In Equation 5-11 ci denotes the concentration of species
i in the liquid (SI unit: mol/m
3),
cP, i the amount adsorbed to (or desorbed from) solid particles (moles per unit dry weight of the solid), and
cG, i the concentration of species
i in the gas phase.
The equation balances the mass transport throughout the porous medium using the porosity εp, the liquid volume fraction
θ; the bulk (or drained) density,
ρb = (1
− εp)
ρ, and the solid phase density
ρ (SI unit: kg/m
3).
For saturated porous media, the liquid volume fraction θ is equal to the porosity
εp, but for partially saturated porous media, they are related by the saturation
s as
θ =
sεp. The resulting gas volume fraction is
av =
εp − θ =
(1-s)εp.
On the right-hand side of Equation 5-11, the first term introduces the spreading of species due to mechanical mixing as well as from diffusion and volatilization to the gas phase. The tensor is denoted
DD (SI unit: m
2/s) and the effective diffusion by
De (SI unit: m
2/s).
The last two terms on the right-hand side of Equation 5-11 describe production or consumption of the species;
Ri is a reaction rate expression which can account for reactions in the liquid, solid, or gas phase, and S
i is an arbitrary source term, for example due to a fluid flow source or sink.
In order to solve for the solute concentration of species i,
ci, the solute mass sorbed to solids
cP,i and dissolved in the gas-phase
cG,i are assumed to be functions of
ci. Expanding the time-dependent terms gives
where kP,i = ∂cP,i/∂ci is the adsorption isotherm and
kG,i = ∂cG,i/∂ci is the linear volatilization.
Equation 5-11 can then be written as