The Segregated Solver
Segregated in the COMSOL Multiphysics Programming Reference Manual
Termination Criterion for a Segregated Solver
For the Solution termination criterion: When termination of the Segregated solver is based on the estimated error, it terminates if, for all the groups j, the error estimate is smaller than the corresponding tolerance,
where the error estimate in segregated iteration k is
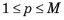
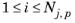
The number tolj is the relative tolerance for the corresponding group. For each degree of freedom (DOF), the field variable solved for is and is the index of that DOF. The largest damped Newton error is then estimated by:
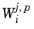
Here l is taken for all iterations in all substeps solving for the group j, αl,j is the damping factor, ΔU l, j, k,p is the Newton increment vector, and Nj,p is the number of DOFs in the field p. The weight factor is described below. Moreover,
is the relative increment over one complete iteration k. In this expression, Uj,k,p is the segregated solution vector for the group j, and
where Si is a scale factor that the solver determines from the settings in the Scaling section of the Settings window for the Dependent Variables node, where the following choices are available in the Method list:
•
For Automatic, Si is the factor 0.1 times the average of |Um| for all DOFs m having the same name as DOF i.
•
For Manual, Si is the value for DOF i given in the Manual scaling field.
•
For Initial value based, Si is the factor 0.1 times the average of |U0m| for all DOFs m having the same name as DOF i, where U0 is the solution vector corresponding to the initial value.
•
For None, Wi = 1.
Si is independent of the field variable p.
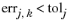
For the Residual termination criterion, the segregated solver terminates when the following convergence criterion is satisfied: For all the groups j, the error estimate is smaller than the corresponding tolerance, , where
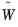
where F is the current residual, and are the weights determined by the first and, if applicable, the second residual. The iterations can also terminate if the relative solution based error is in the range of a hundred machine epsilon.
Pseudo Time Stepping
Pseudo time stepping is available in a stationary segregated approach as well; see Pseudo Time Stepping for a description of the CFL regulation. For the segregated solver, the error estimate en in Equation 19-1 is the arithmetic average of the errors in the different segregated groups.