For the Fully Coupled attribute, you can define one of the settings for the double dogleg method. Also see Termination Criterion for the Fully Coupled and Segregated Attribute Nodes.

The double dogleg method (Ref. 22) is available for stationary problems. It is a Newton trust region method and can as such adjust the direction as well as the step length when solving the nonlinear equation , : .

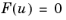
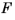
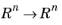
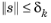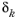
subject to . Here the size of the step s is required to be bounded by the trust region radius . Both the Cauchy point — that is, the minimizer of m in the steepest descent direction — and the Newton point are utilized. In each iteration the algorithm dynamically adjusts the size of the trust region depending on the predicted decrease of m compared to the actual one. The double dogleg step is then given by a certain convex combination of the Cauchy step (steepest descent direction) and the Newton step. For difficult problems you can choose to start the computation by a damped Newton step. Enter the damping factor between 0 and 1 in the Initial damping factor field. The algorithm terminates if the norm of the scaled residual is less than the given tolerance, . 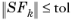You can choose the type of scaling in the Residual scaling list. See the Fully Coupled Method and Termination settings.