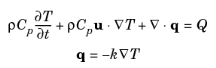The thermal conductivity k describes the relationship between the heat flux vector
q and the temperature gradient
∇T in
q = −k∇T, which is Fourier’s law of heat conduction. Enter this quantity as power per length and temperature.
The default Thermal conductivity k is taken
From material. For
User defined select
Isotropic,
Diagonal,
Symmetric, or
Anisotropic based on the characteristics of the thermal conductivity, and enter another value or expression. For
Isotropic enter a scalar which will be used to define a diagonal tensor. For the other options, enter values or expressions into the editable fields of the tensor.
The components of the thermal conductivity k when given on tensor form (
kxx,
kyy, and so on, representing an anisotropic thermal conductivity) are available as
ht.kxx,
ht.kyy, and so on (using the default name
ht). The single scalar mean effective thermal conductivity
ht.kmean is the mean value of the diagonal elements
kxx,
kyy, and
kzz.
The heat capacity at constant pressure describes the amount of heat energy required to produce a unit temperature change in a unit mass.
In addition, the thermal diffusivity α, defined as
k ⁄ (
ρ Cp) (SI unit: m
2/s), is also a predefined quantity. The thermal diffusivity can be interpreted as a measure of thermal inertia (heat propagates slowly where the thermal diffusivity is low, for example). The components of the thermal diffusivity
α, when given on tensor form (
αxx,
αyy, and so on, representing an anisotropic thermal diffusivity) are available as
ht.alphaTdxx,
ht.alphaTdyy, and so on (using the default physics name
ht). The single scalar mean thermal diffusivity
ht.alphaTdMean is the mean value of the diagonal elements
αxx,
αyy, and
αzz. The denominator
ρ Cp is the effective volumetric heat capacity which is also available as a predefined quantity,
ht.C_eff.